Next: Beyond B-splines
Up: Interpolation with convolutional bases
Previous: B-splines
For completeness, I include a 2-D forward interpolation example.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a 2-D analog of the function in
Figure
shows a 2-D analog of the function in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and its coarsely-sampled version.
and its coarsely-sampled version.
chirp2
Figure 21 Two-dimensional test function
(left) and its coarsely sampled version (right).





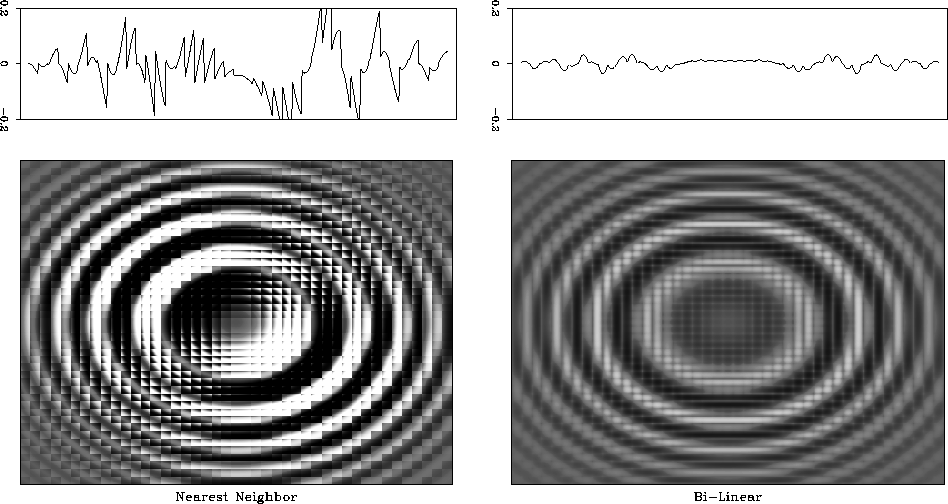
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the errors of the 2-D nearest
neighbor and 2-D linear (bi-linear) interpolation. Switching to
bi-linear interpolation shows a significant improvement, but the error
level is still relatively high. As shown in
Figures
compares the errors of the 2-D nearest
neighbor and 2-D linear (bi-linear) interpolation. Switching to
bi-linear interpolation shows a significant improvement, but the error
level is still relatively high. As shown in
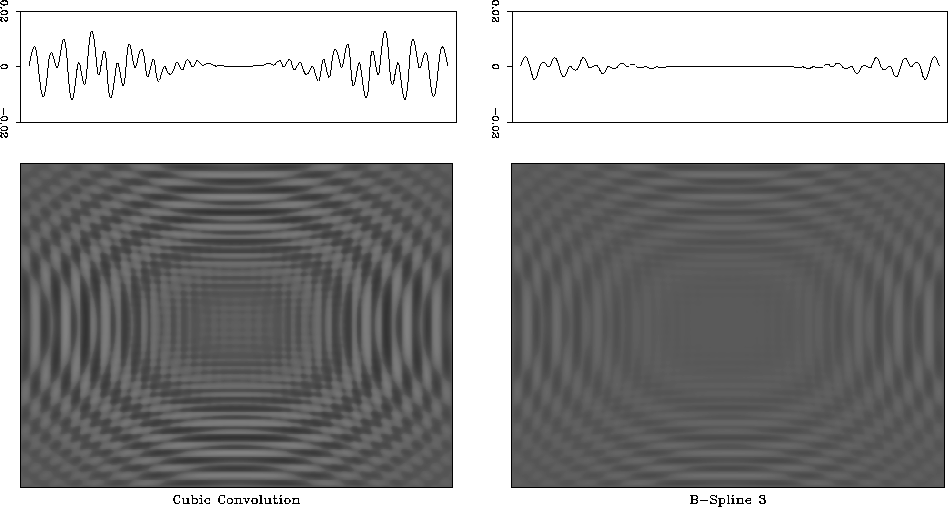
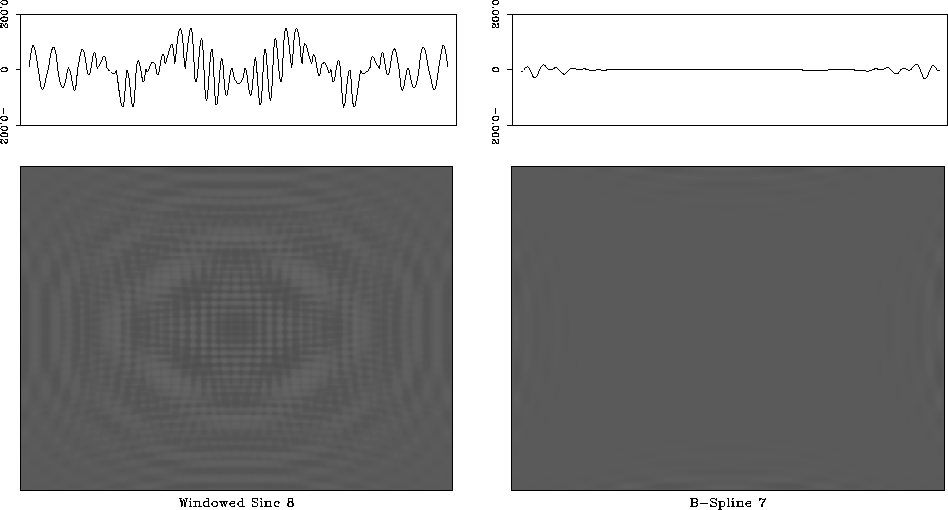
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , B-spline
interpolation again outperforms other methods with comparable cost. In
all cases, I constructed 2-D interpolants by orthogonal splitting.
Although the splitting method reduces computational overhead, the main
cost factor is the total interpolant size, which is squared when the
interpolation goes from one to two dimensions.
, B-spline
interpolation again outperforms other methods with comparable cost. In
all cases, I constructed 2-D interpolants by orthogonal splitting.
Although the splitting method reduces computational overhead, the main
cost factor is the total interpolant size, which is squared when the
interpolation goes from one to two dimensions.
plcbinlin
Figure 22 2-D Interpolation errors of
nearest neighbor interpolation (left) and linear interpolation
(right). The top graphs show 1-D slices through the center of the
image. Bi-linear interpolation exhibits smaller error and therefore
is more accurate.




 plccubspl
plccubspl
Figure 23 2-D Interpolation errors of
cubic convolution interpolation (left) and third-order B-spline
interpolation (right). The top graphs show 1-D slices through the
center of the image. B-spline interpolation exhibits smaller error
and therefore is more accurate.




 plckaispl
plckaispl
Figure 24 2-D Interpolation errors of
8-point windowed sinc interpolation (left) and seventh-order
B-spline interpolation (right). The top graphs show 1-D slices
through the center of the images. B-spline interpolation exhibits
smaller error and therefore is more accurate.










Next: Beyond B-splines
Up: Interpolation with convolutional bases
Previous: B-splines
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a 2-D analog of the function in
Figure
shows a 2-D analog of the function in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and its coarsely-sampled version.
and its coarsely-sampled version.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a 2-D analog of the function in
Figure
shows a 2-D analog of the function in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and its coarsely-sampled version.
and its coarsely-sampled version.

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the errors of the 2-D nearest
neighbor and 2-D linear (bi-linear) interpolation. Switching to
bi-linear interpolation shows a significant improvement, but the error
level is still relatively high. As shown in
Figures
compares the errors of the 2-D nearest
neighbor and 2-D linear (bi-linear) interpolation. Switching to
bi-linear interpolation shows a significant improvement, but the error
level is still relatively high. As shown in
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , B-spline
interpolation again outperforms other methods with comparable cost. In
all cases, I constructed 2-D interpolants by orthogonal splitting.
Although the splitting method reduces computational overhead, the main
cost factor is the total interpolant size, which is squared when the
interpolation goes from one to two dimensions.
, B-spline
interpolation again outperforms other methods with comparable cost. In
all cases, I constructed 2-D interpolants by orthogonal splitting.
Although the splitting method reduces computational overhead, the main
cost factor is the total interpolant size, which is squared when the
interpolation goes from one to two dimensions.