




Next: Overview of thesis
Up: Tomography
Previous: Non-linear problems
If the model space is a uniformally sampled
Cartesian mesh or something similar, we face
another problem when doing reflection tomography,
its large null space.
There are several reasons for this null space:
- shadow zones
- Certain parts of the velocity model simply
might not be illuminated, or illuminated poorly by the acquisition
geometry.
A classical example is under the edge of a salt body ().
- limited angle coverage
- The recording geometry imposes a limitation on vertical resolution.
The left panel of Figure 5 simulates a ray-based back
projection operator. Along each ray a random slowness change
is back projected. The right panel of Figure 5 shows
the Fourier response. Note how large wavenumbers in z are not
well illuminated. Often this phenomenon is explained in terms
of the Fourier slice theorem.
The Fourier transform of a vertical projection in space is a horizontal
radial profile.
slice
Figure 5 The left panel simulates a ray-based back
projection operator. Along each ray a random slowness change
is back projected. The right panel shows
the Fourier response.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





- resolution decreases with depth
- When the reflection point is unknown, normal angle reflection times
do not contain any information about velocity. As the reflection angle
increases, velocity discrimination becomes easier.
At larger depths, given the limited surface
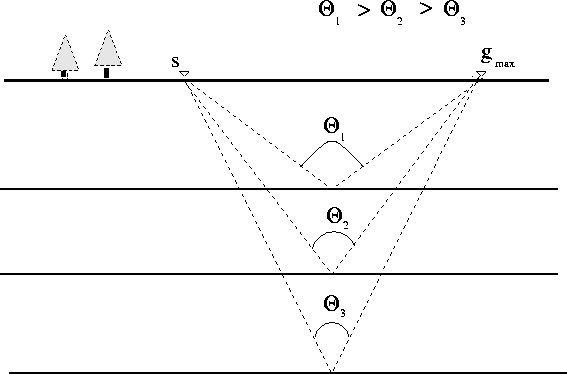
recording geometry, the angle coverage will decrease (Figure 6).
As a result, larger depth model components are often under- or unilluminated
().
If we follow the Fourier analysis of Figure 5 we can see
that the vertical resolution decreases as the reflector depth increases (Figure 7).
ray-limit
Figure 6 Given a fixed recording geometry (s being the source
and 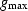 being the farthest
receiver) as we go deeper in depth the angle range that we at
each reflector decreases. being the farthest
receiver) as we go deeper in depth the angle range that we at
each reflector decreases.
|
|  |
 slice.depth
slice.depth
Figure 7 Left panel shows simulated
raypaths with random energy introduced along each raypath. The right panel
is the Fourier response. From top to bottom the depth of the reflector
increases.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





- not enough equations
- In most reflection tomography methods, we invert a limited set
of positioning errors. When doing tomography, especially 3-D tomography,
it is possible to have more model points than moveout errors.
To deal with
the null space of the reflection tomography operator
there are two alternative paths
that could be followed, reparameterization or regularization.
Reparameterization can be done by a coarser sampling of the Cartesian, but
usually involves other parameterizations of the model space.
It
usually takes the form of either a layered model with simple velocity function
(such as velocity gradient) within the layers ()
or reparameterizing the model
in term of
spline nodes ().
The layered model approach is attractive because
it allows a linking between an interpreter's
geologic model (). It also provides a fairly accurate
description of velocity structure in regions such as the North Sea.
The spline node approach can also be beneficial. It can guarantee
the velocity model will be smooth (necessary for ray based methods)
and with selective placement of nodes can
allow less freedom in areas where the data provides less information about the
velocity field.
The downside of both of these approaches is that the parameterization
must be chosen a priori. At early iterations the guess
at the velocity model can be in significant error. If we do
a poor job of parameterizing the model we
could actually slow, or stop, the problem from converging ().
The second option is regularization.
In the regularization approach we add a second term
to the objective function,
where  penalizes some definition of roughness in the model.
The regularization approach has its own drawbacks. The most significant
is that the resulting model space may no longer has any direct connection with
geology. In addition, choosing
penalizes some definition of roughness in the model.
The regularization approach has its own drawbacks. The most significant
is that the resulting model space may no longer has any direct connection with
geology. In addition, choosing  is problematic and
can introduce unrealistic elements into the slowness estimate.
is problematic and
can introduce unrealistic elements into the slowness estimate.





Next: Overview of thesis
Up: Tomography
Previous: Non-linear problems
Stanford Exploration Project
4/29/2001

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)


![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)