




Next: Test example
Up: Inverse Interpolation and Data
Previous: Inverse Interpolation and Data
In many cases, the regularization (styling) condition originates in a
continuous differential operator. For example, one can think of the
gradient or Laplacian operator for regularizing smooth functions
Fomel (2000b), plane-wave destructor for regularizing
local plane waves Fomel (2000a), or the offset
continuation equation for regularizing seismic reflection data
Fomel (2000c).
Let us denote the continuous regularization operator by D.
Regularization implies seeking a function f(x) such that the
least-squares norm of ![$D\left[f(x)\right]$](img40.gif) is minimum. Using the usual
expression for the least-squares norm of continuous functions and
substituting the basis decomposition (8), we obtain
the expression
is minimum. Using the usual
expression for the least-squares norm of continuous functions and
substituting the basis decomposition (8), we obtain
the expression
| ![\begin{displaymath}
\left\Vert D\left[f(x)\right]\right\Vert =
\int \left(D\l...
...t(\sum_{k \in K} c_k D\left[ \beta (x-k)\right]\right)^2\,dx\;.\end{displaymath}](img41.gif) |
(22) |
The problem of finding function f(x) reduces to the problem of
finding the corresponding set of basis coefficients ck. We can
obtain the solution to the least-squares optimization by
differentiating the quadratic objective function (22) with
respect to the basis coefficients ck. This leads to the system of
linear equations
| ![\begin{displaymath}
\sum_{k \in K} c_k \int D \left[\beta (x-k)\right]
D\left[\beta (x-j)\right] \,dx =
\sum_{k \in K} c_k d_{j-k} = 0\;,\end{displaymath}](img42.gif) |
(23) |
where
| ![\begin{displaymath}
d_j = \int D\left[\beta (x)\right] D\left[\beta (x-j)\right]\,dx\;.\end{displaymath}](img43.gif) |
(24) |
Equation (23) is clearly a discrete convolution of the
spline coefficients ck with the filter dj defined in
equation (24). To transform the system (23) to a
regularization condition of the form
| 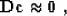 |
(25) |
we need to treat the digital filter dj as an autocorrelation and
find its minimum-phase factor. Equation (25) replaces
equation (20) in the inverse interpolation problem setting.
We have found a constructive way of creating B-spline regularization
operators from continuous differential equations.
A simple regularization example is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The continuous operator D in this case comes from the theoretical
plane-wave differential equation. I constructed the auto-correlation
filter dj according to formula (24) and factorized it
with the efficient Wilson-Burg method on a helix
Sava et al. (1998). The figure shows three plane waves
constructed from three distant spikes by applying an inverse recursive
filtering with two different plane-wave regularizers. The left plot
corresponds to using first-order B-splines (equivalent to linear
interpolation). This type of regularizer is identical to Clapp's
steering filters Clapp et al. (1997) and suffers from numerical
dispersion effects. The right plot was obtained with third-order
splines. Most of the dispersion is suppressed by using a more accurate
interpolation.
.
The continuous operator D in this case comes from the theoretical
plane-wave differential equation. I constructed the auto-correlation
filter dj according to formula (24) and factorized it
with the efficient Wilson-Burg method on a helix
Sava et al. (1998). The figure shows three plane waves
constructed from three distant spikes by applying an inverse recursive
filtering with two different plane-wave regularizers. The left plot
corresponds to using first-order B-splines (equivalent to linear
interpolation). This type of regularizer is identical to Clapp's
steering filters Clapp et al. (1997) and suffers from numerical
dispersion effects. The right plot was obtained with third-order
splines. Most of the dispersion is suppressed by using a more accurate
interpolation.
sthree
Figure 28 B-spline regularization. Three
plane waves constructed by 2-D recursive filtering with the B-spline
plane-wave regularizer. Left: using first-order B-splines (linear
interpolation). Right: using third-order B-splines.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Test example
Up: Inverse Interpolation and Data
Previous: Inverse Interpolation and Data
Stanford Exploration Project
9/5/2000
![]() is minimum. Using the usual
expression for the least-squares norm of continuous functions and
substituting the basis decomposition (8), we obtain
the expression
is minimum. Using the usual
expression for the least-squares norm of continuous functions and
substituting the basis decomposition (8), we obtain
the expression
![\begin{displaymath}
\left\Vert D\left[f(x)\right]\right\Vert =
\int \left(D\l...
...t(\sum_{k \in K} c_k D\left[ \beta (x-k)\right]\right)^2\,dx\;.\end{displaymath}](img41.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The continuous operator D in this case comes from the theoretical
plane-wave differential equation. I constructed the auto-correlation
filter dj according to formula (24) and factorized it
with the efficient Wilson-Burg method on a helix
Sava et al. (1998). The figure shows three plane waves
constructed from three distant spikes by applying an inverse recursive
filtering with two different plane-wave regularizers. The left plot
corresponds to using first-order B-splines (equivalent to linear
interpolation). This type of regularizer is identical to Clapp's
steering filters Clapp et al. (1997) and suffers from numerical
dispersion effects. The right plot was obtained with third-order
splines. Most of the dispersion is suppressed by using a more accurate
interpolation.
.
The continuous operator D in this case comes from the theoretical
plane-wave differential equation. I constructed the auto-correlation
filter dj according to formula (24) and factorized it
with the efficient Wilson-Burg method on a helix
Sava et al. (1998). The figure shows three plane waves
constructed from three distant spikes by applying an inverse recursive
filtering with two different plane-wave regularizers. The left plot
corresponds to using first-order B-splines (equivalent to linear
interpolation). This type of regularizer is identical to Clapp's
steering filters Clapp et al. (1997) and suffers from numerical
dispersion effects. The right plot was obtained with third-order
splines. Most of the dispersion is suppressed by using a more accurate
interpolation.

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)