Next: NUMERICAL RESULTS
Up: Theory of daylight imaging
Previous: Source location imaging
To image the unknown scatterer location and strength at 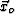 , we
simply identify the migration operator which, when applied
to the crosscorrelated data in equation (4), cancels the
phase of the
, we
simply identify the migration operator which, when applied
to the crosscorrelated data in equation (4), cancels the
phase of the 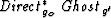 term.
Such a migration operator is given by
term.
Such a migration operator is given by
| 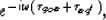 |
(3) |
where x and go denote, respectively, the trial scatterer
and specular-reflector point locations respectively.
Application of this migration operator to equation (3)
will annihilate the phase term of the 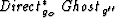 term in equation (3) when both
the trial image point,
term in equation (3) when both
the trial image point, 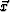 , coincides with the actual source
location denoted by
, coincides with the actual source
location denoted by 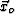 , and the trial
specular-reflection point,
, and the trial
specular-reflection point, 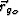 , coincides with the actual
specular-reflection point,
, coincides with the actual
specular-reflection point, 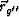 . In other words, we require
both
. In other words, we require
both
| 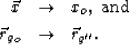 |
(4) |
| (5) |
This can be understood more clearly by noting that
the migrated reflectivity section is given by summation of the
migrated crosscorrelation data over all geophone pairs
As 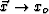 and as
and as 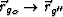 , then it is clear that the above phase goes to zero, leading
to constructive interference at the scatterer's location.
In practice, these two conditions will be fulfilled if the
specular-reflection point is within the aperture of the recording
array and the geophone array is sufficiently dense.
fig2
, then it is clear that the above phase goes to zero, leading
to constructive interference at the scatterer's location.
In practice, these two conditions will be fulfilled if the
specular-reflection point is within the aperture of the recording
array and the geophone array is sufficiently dense.
fig2
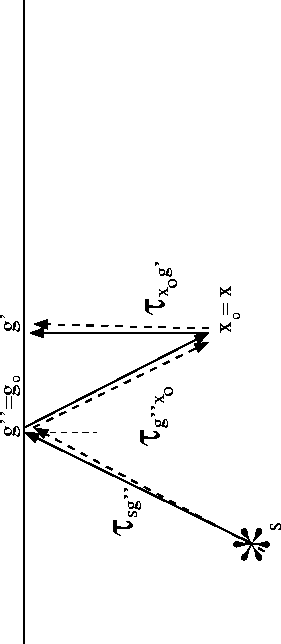
Figure 2
Ghost reflection rays associated with
a source at s, a trial image point
at x, and a scatterer at xo.

fig3
Figure 3
As x approaches x0 and go approaches g'' in
Figure 2, the dashed rays coincide with the solid
rays.
Thus the Direct Ghost correlation term will have zero phase,
leading to maximal constructive interference of the migration section
at the actual scatterer point.






Next: NUMERICAL RESULTS
Up: Theory of daylight imaging
Previous: Source location imaging
Stanford Exploration Project
9/5/2000
![\begin{eqnarray}
m_{\rm refl}(\vec x, \omega) &=& \sum_{g_o} \sum_{g'} \;
W(\vec...
...x }-
\tau_{xg'})} + {\rm\it all~other~terms} \right]. \nonumber\ \end{eqnarray}](img27.gif)