Next: Reflectivity distribution imaging
Up: Theory of daylight imaging
Previous: Theory of daylight imaging
To image the unknown source location at 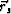 from the data
given in equation (3), we
simply identify the migration operator which when applied
to the above equation cancels the phase of the
from the data
given in equation (3), we
simply identify the migration operator which when applied
to the above equation cancels the phase of the
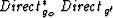 term.
Such a migration operator is given by
term.
Such a migration operator is given by
| 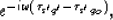 |
(2) |
where s' denotes the trial source-point location.
Application of this migration operator to the crosscorrelated data in
equation (3) will annihilate
the phase of the 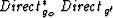 term
when the trial image point
term
when the trial image point 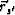 coincides with the actual source location denoted by
coincides with the actual source location denoted by 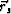 .The migration section is then given by summation over all geophone pairs
.The migration section is then given by summation over all geophone pairs
The migration operator in equation (5) is "tuned" to
image the source location so that as
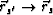 , the
, the 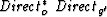 term will
constructively interfere while the all other terms tend to
cancel.
term will
constructively interfere while the all other terms tend to
cancel.
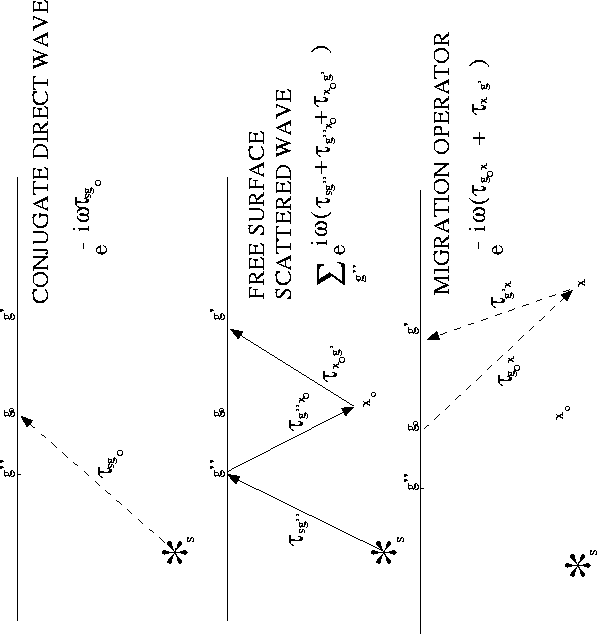
fig1
Figure 1
(Top) Direct ray and a (middle) scattered ray excited by
a specular free-surface reflection associated with a source at
s and a scatterer at xo.
Bottom figure denotes the
rays associated with the migration operator
for free-surface reflections.






Next: Reflectivity distribution imaging
Up: Theory of daylight imaging
Previous: Theory of daylight imaging
Stanford Exploration Project
9/5/2000
![\begin{eqnarray}
m_{\rm source}(\vec r_{s'},\omega) &=&
\sum_{g_o} \sum_{g'} \;...
...+ \tau_{s'g_o })} + {\rm\it all~other~terms} \right].
\nonumber\ \end{eqnarray}](img18.gif)
![]() , the
, the ![]() term will
constructively interfere while the all other terms tend to
cancel.
term will
constructively interfere while the all other terms tend to
cancel.