




Next: Results
Up: Background
Previous: Multiscale regularization
The quadtree decomposition is an adaptive sampling scheme which seeks to divide a digital image
into regions of nearly homogeneous pixel value. Intuitively, the block size is smallest where
the image changes most rapidly, and largest where the pixel values are constant over large
areas.
A similar intuition applies to the interpolation of sparse data.
Given point data collected on the Earth's surface, equation (1) relates
how the data is placed into the discrete computational grid. If data is collected
at perfectly regular intervals on the Earth's surface, it is possible to choose a bin
size such that one and only one measurement falls in each bin. On the other hand, if
the data sampling is irregular, two problems may arise: 1) more than one datum may fall
into a given bin, and the values averaged, implying information loss, and 2) no data may
fall into a given bin, leaving a ``hole'' in the model.
Applied to interpolation, the quadtree methodology seeks to adaptively sample the model
such that 1) where data are closely spaced, the bin size is small, to minimize averaging
of adjacent data and 2) where data are sparsely distributed, the bin size is large, to
avoid introducing holes in the model.
First assume that there exists a regular bin size
such that binning the data produces a model with no holes. From here, we regard
``bin size'' as equivalent to ``scale'' - where scale goes from coarsest (largest bins) to
finest (smallest bins). Also assume that at each scale, the bins which contain one or more
data values are known.
-
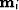 - Model at scale i; i=0 is coarsest scale, i=n is finest scale.
- Model at scale i; i=0 is coarsest scale, i=n is finest scale.
-
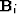 - Bin data onto grid of scale i; i=0 is coarsest scale, i=n is
finest scale.
- Bin data onto grid of scale i; i=0 is coarsest scale, i=n is
finest scale.
-
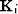 - Known data mask at scale i - 1 for bins which contain data, 0 otherwise;
i=0 is coarsest scale, i=n is finest scale.
- Known data mask at scale i - 1 for bins which contain data, 0 otherwise;
i=0 is coarsest scale, i=n is finest scale.
-
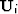 - Upsampling operator. Upsample from scale i-1 to scale i.
i=0 is coarsest scale, i=n is finest scale. Adjoint to
the downsampling operator in the multiscale regularization discussion. For
instance, if the downsampling operator sums four input bin locations into
an output location and averages, the upsampling operator takes the averaged
value and places it back into the four bins.
- Upsampling operator. Upsample from scale i-1 to scale i.
i=0 is coarsest scale, i=n is finest scale. Adjoint to
the downsampling operator in the multiscale regularization discussion. For
instance, if the downsampling operator sums four input bin locations into
an output location and averages, the upsampling operator takes the averaged
value and places it back into the four bins.
-
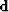 - data.
- data.
The algorithm proceeds as follows.
- 1.
- Compute
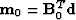 .
. - 2.
- Loop over scale:
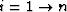 .
. - 3.
- Upsample
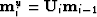 .
. - 4.
- Compute
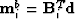 .
. - 5.
- Where
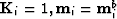 . Otherwise,
. Otherwise, 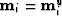 .
. - 6.
- End Loop.
This approach is quite similar to the Multigrid-style method employed by Crawley (1995),
but there is no inversion involved - my method is totally explicit.
Interestingly, Luettgen et al. (1994) show that for the underdetermined optical flow determination
problem of image processing, use of an explicit quadtree scheme gives results identical by some
measures to the result obtained by solving a regularized inverse problem.





Next: Results
Up: Background
Previous: Multiscale regularization
Stanford Exploration Project
9/5/2000