Next: Discussion
Up: Brown: Sparse data interpolation
Previous: Quadtree Pyramid Interpolation
In this paper, I use a particularly simple example dataset - a 10-meter-resolution digital
elevation map (DEM) of the area surrounding Fallen Leaf Lake, obtained freely from
USGS![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) . This map, along with some
relevant landforms, is shown in Figure
. This map, along with some
relevant landforms, is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
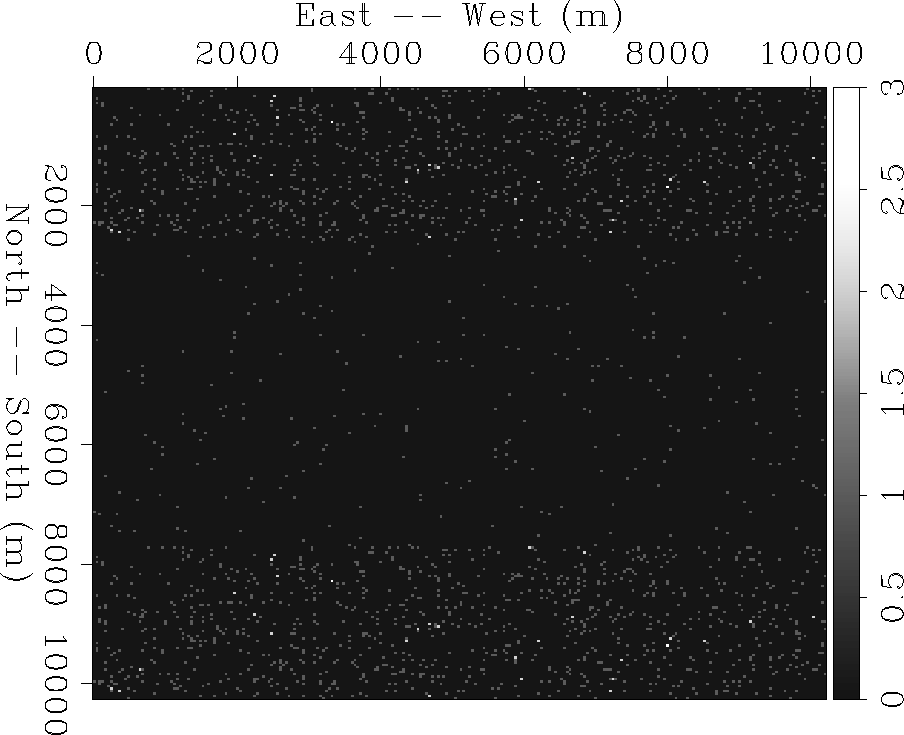
To simulate an experiment, I sampled the map randomly at 2250 points:
1000 points in the northern region, 1000 in the southern region, and only 250 in the
central region.
The model grid is 256x256 points, giving a 40-meter output resolution.
Figure
.
To simulate an experiment, I sampled the map randomly at 2250 points:
1000 points in the northern region, 1000 in the southern region, and only 250 in the
central region.
The model grid is 256x256 points, giving a 40-meter output resolution.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the experiment's fold, which varies from 0 to 3.
topo2
shows the experiment's fold, which varies from 0 to 3.
topo2
Figure 1 Left: Digital elevation map of the vicinity around
Fallen Leaf Lake, California. Resolution is 10 meters. Windowed down from an original
size of roughly 1400x1200 points to 1024x1024 points. Right: North-south derivative applied to
topography to highlight landforms.





topo2-fold
Figure 2 Experimental fold. 2250 random samples on the
1024x1024 map are the ``data''. Model grid is 256x256.





Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) through
through ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the results
of applying various estimation schemes to fill the holes in the acquisition. Starting from
upper-left and moving clockwise, each of the four figures shows a) the ``answer,'' i.e., the
1024x1024 topographical surface, subsampled by a factor of four, b) the estimated model,
c) The error in the estimate clipped to a common value and overlain by the the 2250 known data
locations, and d) a crossplot of the estimated model and answer at 4000 randomly chosen spatial
locations.
show the results
of applying various estimation schemes to fill the holes in the acquisition. Starting from
upper-left and moving clockwise, each of the four figures shows a) the ``answer,'' i.e., the
1024x1024 topographical surface, subsampled by a factor of four, b) the estimated model,
c) The error in the estimate clipped to a common value and overlain by the the 2250 known data
locations, and d) a crossplot of the estimated model and answer at 4000 randomly chosen spatial
locations.
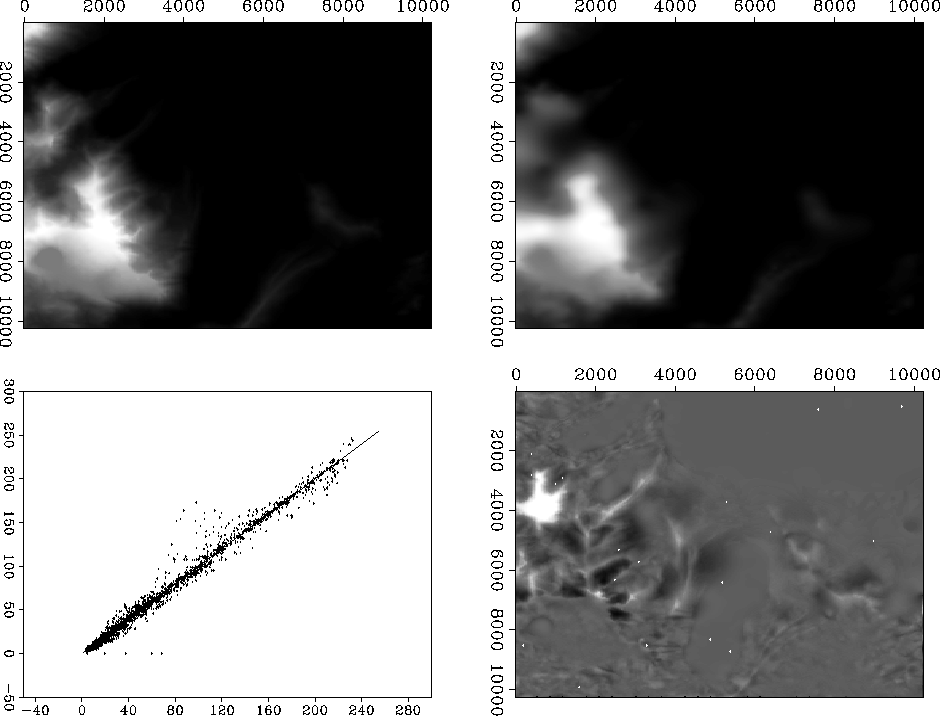
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows 100 iterations with Laplacian regularization.
Obviously, convergence has not been achieved.
Figure
shows 100 iterations with Laplacian regularization.
Obviously, convergence has not been achieved.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows 1000 iterations with Laplacian regularization.
The crossplot is very tight, making this result tough to beat.
Figure
shows 1000 iterations with Laplacian regularization.
The crossplot is very tight, making this result tough to beat.
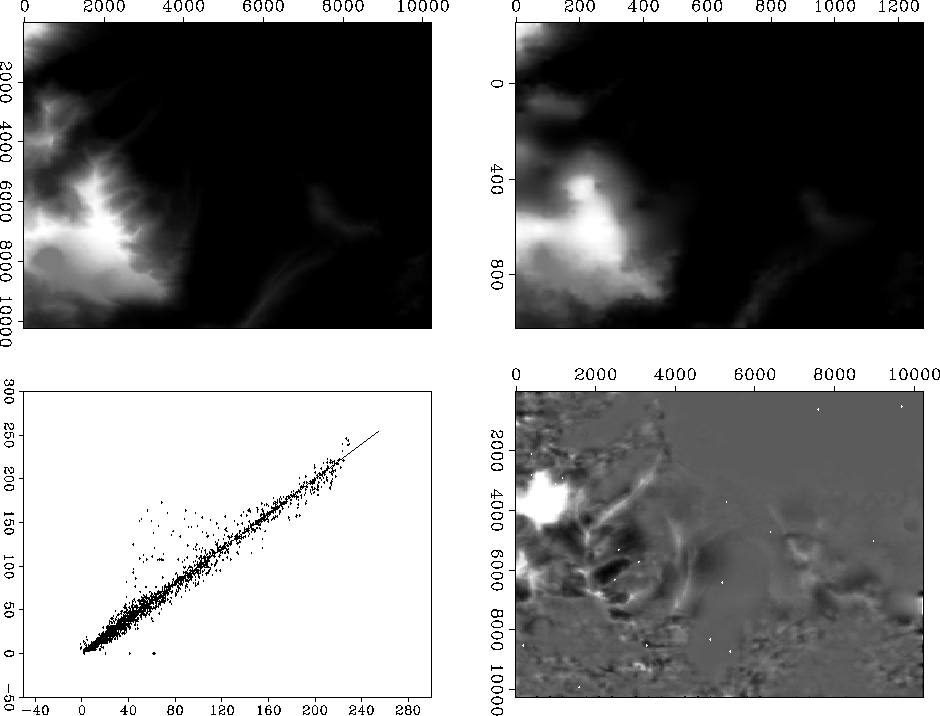
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows 100 iterations of Laplacian regularization with preconditioning.
This result is disappointing: Convergence to this result occured in only 10-20 iterations, but the result
itself is not desirable. Although not the subject of this paper, the ``ice-cream-cone'' nature of this result
is alarming and merits further investigation.
Figure
shows 100 iterations of Laplacian regularization with preconditioning.
This result is disappointing: Convergence to this result occured in only 10-20 iterations, but the result
itself is not desirable. Although not the subject of this paper, the ``ice-cream-cone'' nature of this result
is alarming and merits further investigation.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows 100 iterations of multiscale Laplacian regularization.
This result is quite similar to the 1000 iterations Lapacian result, but the crossplot is
not as tight. Also, we expect this result to be a bit smoother than the pure Laplacian,
but it is difficult to see if it is.
Figure
shows 100 iterations of multiscale Laplacian regularization.
This result is quite similar to the 1000 iterations Lapacian result, but the crossplot is
not as tight. Also, we expect this result to be a bit smoother than the pure Laplacian,
but it is difficult to see if it is.
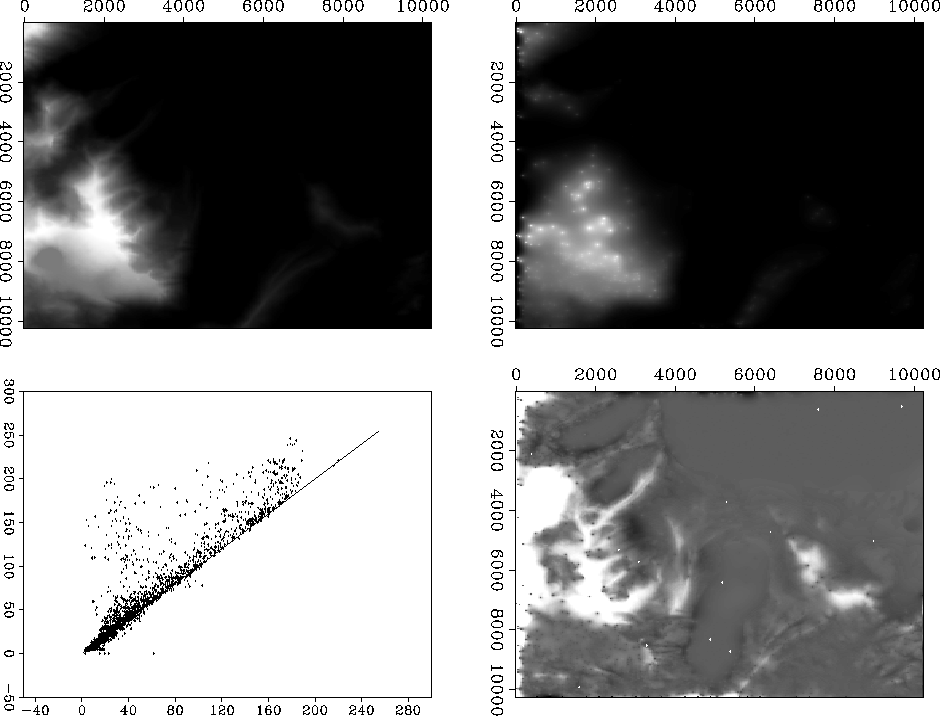
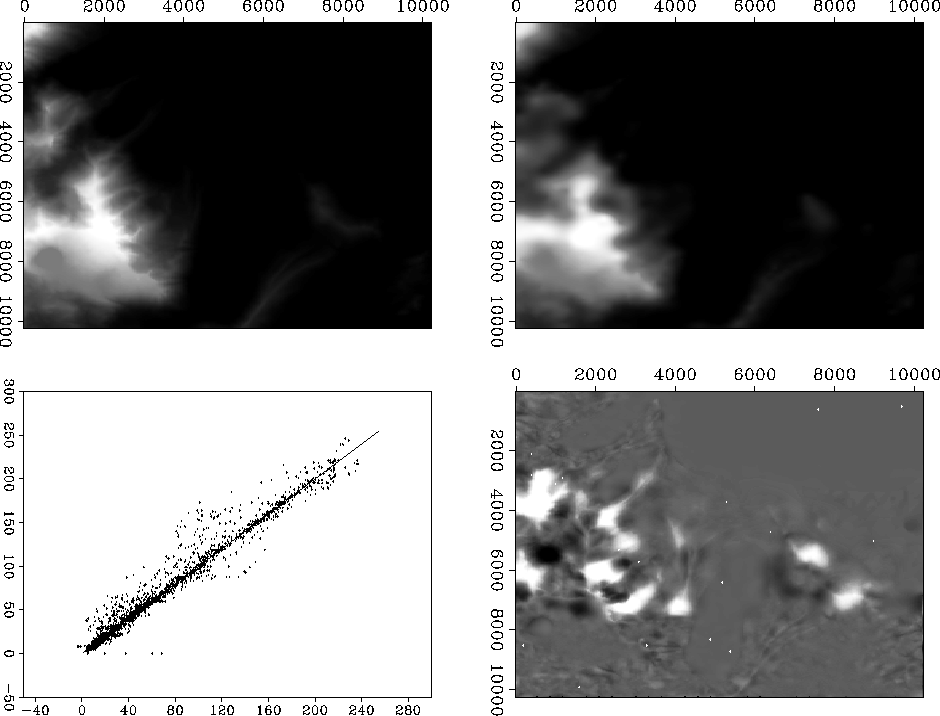
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the explicit Quadtree Pyramid interpolation.
The quadtree structure of the result is quite apparent. Although the interpolated map is not
smooth spatially, the general structure of the topography are reproduced quite convincingly.
Figure
shows the explicit Quadtree Pyramid interpolation.
The quadtree structure of the result is quite apparent. Although the interpolated map is not
smooth spatially, the general structure of the topography are reproduced quite convincingly.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows 100 iterations of Laplacian regularization, with
the explicit Quadtree Pyramid interpolation (Figure
shows 100 iterations of Laplacian regularization, with
the explicit Quadtree Pyramid interpolation (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) used as a starting guess.
This result is quite similar to the 1000 iterations Laplacian result; also the 100 iterations with the
multiscale Laplacian.
) used as a starting guess.
This result is quite similar to the 1000 iterations Laplacian result; also the 100 iterations with the
multiscale Laplacian.
topodata2-lap100-show
Figure 3 Simple Laplacian regularization, 100 iterations.
Clockwise from upper-left: True model; Estimated model; Error; Crossplot of true versus estimated model.





topodata2-lap1000-show
Figure 4 Laplacian regularization, 1000 iterations.
Clockwise from upper-left: True model; Estimated model; Error; Crossplot of true versus estimated model.





topodata2-prec100-show
Figure 5 Preconditioned Laplacian regularization, 100 iterations.
Clockwise from upper-left: True model; Estimated model; Error; Crossplot of true versus estimated model.





topodata2-ms100-show
Figure 6 Multiscale Laplacian regularization, 100 iterations.
Clockwise from upper-left: True model; Estimated model; Error; Crossplot of true versus estimated model.





topodata2-pyramid-show
Figure 7 Quadtree pyramid interpolation result.
Clockwise from upper-left: True model; Estimated model; Error; Crossplot of true versus estimated model.





topodata2-pyrlap100-show
Figure 8 Laplacian regularization, 100 iterations.
Clockwise from upper-left: True model; Estimated model; Error; Crossplot of true versus estimated model.





As the ``answer'' is known in this problem, we can quantitatively check the accuracy of an estimated
model. The statistics below speak for themselves.
Taking the standard deviation of the error to be a measure of goodness, we can rank the results from
best to worst:
- 1.
- Laplacian regularization, 1000 iterations.
- 2.
- Multiscale Laplacian regularization, 100 iterations.
- 3.
- Laplacian regularization, 100 iterations, quadtree pyramid interpolation used as starting guess.
- 4.
- Quadtree pyramid direct interpolation.
- 5.
- Preconditioned Laplacian regularization, 100 iterations.
- 6.
- Laplacian regularization, 100 iterations.
Laplacian regularization, 100 iterations
| Min. Val. | Max. Val. | Mean Val. | Median | Std. Dev. |
----------------------------------------
True values: -42.10075 253.25171 33.82695 12.50521 48.19902
Estimated values: 0.00000 246.00000 44.96923 18.00000 54.02688
Errors: -70.55768 235.33752 11.14226 0.87845 29.06191
Absolute errors: 0.00000 235.33752 12.89230 2.21318 28.32898
Relative errors: 0.00000 1206.58191 3.02346 0.06742 33.63662
Laplacian regularization, 1000 iterations
| Min. Val. | Max. Val. | Mean Val. | Median | Std. Dev. |
----------------------------------------
True values: 3.19786 232.39223 45.01379 20.00496 53.70287
Estimated values: 0.00000 246.00000 44.96923 18.00000 54.02688
Errors: -68.31208 76.44979 -0.04465 -0.00007 5.77580
Absolute errors: 0.00000 76.44979 2.51392 0.80804 5.20023
Relative errors: 0.00000 1.00000 0.06820 0.02891 0.10538
Preconditioned Laplacian regularization, 100 iterations
| Min. Val. | Max. Val. | Mean Val. | Median | Std. Dev. |
----------------------------------------
True values: 2.55815 220.00000 38.08480 18.64038 45.06718
Estimated values: 0.00000 246.00000 44.96923 18.00000 54.02688
Errors: -61.61859 174.82333 6.88441 0.54753 19.72276
Absolute errors: 0.00000 174.82333 8.05753 1.45995 19.27327
Relative errors: 0.00000 43.94756 0.26195 0.07687 1.28934
Multiscale Laplacian regularization, 100 iterations
| Min. Val. | Max. Val. | Mean Val. | Median | Std. Dev. |
----------------------------------------
True values: -1.53884 229.31610 44.82654 20.00943 53.62170
Estimated values: 0.00000 246.00000 44.96923 18.00000 54.02688
Errors: -62.51950 107.75475 0.14272 -0.00067 8.23634
Absolute errors: 0.00000 107.75475 3.38367 1.06108 7.51047
Relative errors: 0.00000 7.89127 0.09558 0.03850 0.23027
Quadtree pyramid interpolation
| Min. Val. | Max. Val. | Mean Val. | Median | Std. Dev. |
----------------------------------------
True values: 0.00000 235.00000 42.54507 18.00000 52.90804
Estimated values: 0.00000 246.00000 44.96923 18.00000 54.02688
Errors: -77.00000 102.00000 2.42414 0.00000 12.79912
Absolute errors: 0.00000 102.00000 6.17795 1.00000 11.46838
Relative errors: 0.00000 5.82759 0.18037 0.04881 0.40353
Laplacian regularization, 100 iterations, Quadtree pyramid starting guess
| Min. Val. | Max. Val. | Mean Val. | Median | Std. Dev. |
----------------------------------------
True values: -3.58206 237.56772 43.53872 18.33733 53.00369
Estimated values: 0.00000 246.00000 44.96923 18.00000 54.02688
Errors: -68.67423 71.94943 1.43058 0.00038 8.61643
Absolute errors: 0.00000 71.94943 3.64835 0.85361 7.93589
Relative errors: 0.00000 9.47873 0.10503 0.03159 0.31080





Next: Discussion
Up: Brown: Sparse data interpolation
Previous: Quadtree Pyramid Interpolation
Stanford Exploration Project
9/5/2000

![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) . This map, along with some
relevant landforms, is shown in Figure
. This map, along with some
relevant landforms, is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
To simulate an experiment, I sampled the map randomly at 2250 points:
1000 points in the northern region, 1000 in the southern region, and only 250 in the
central region.
The model grid is 256x256 points, giving a 40-meter output resolution.
Figure
.
To simulate an experiment, I sampled the map randomly at 2250 points:
1000 points in the northern region, 1000 in the southern region, and only 250 in the
central region.
The model grid is 256x256 points, giving a 40-meter output resolution.
Figure