




Next: Quadtree Pyramid Interpolation
Up: Background
Previous: Preconditioning
Another approach to combat the slow convergence of least squares sparse data interpolation is
to design a regularization operator that works at multiple scales simultaneously.
Starting with equation (3), we replace the regularization operator, 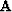 ,
with a composite regularization operator (for the two-scale case):
,
with a composite regularization operator (for the two-scale case):
| ![\begin{displaymath}
\left[\begin{array}
{c}
\bf A \ {\bf AD}_k
\end{array}\right]
\end{displaymath}](img24.gif) |
(8) |
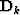 , mnemonic for downsampling, is a normalized binning operator which subsamples a
vector of size n to a vector of size n/k, implicitly smoothing it in the process.
Replacing
, mnemonic for downsampling, is a normalized binning operator which subsamples a
vector of size n to a vector of size n/k, implicitly smoothing it in the process.
Replacing 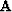 in equation (3) with this new regularization operator gives
in equation (3) with this new regularization operator gives
| ![\begin{displaymath}
\bf
\left[ \begin{array}
{c}
\bf B \ \epsilon_1 \bf A \...
...rray}
{c}
\bf d \ \bf 0 \
\bf 0
\end{array} \right].
\end{displaymath}](img26.gif) |
(9) |
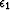 and
and 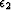 are scaling factors.
In the fashion of equation (4), we can write the least squares inverse corresponding
to the system of equation (9):
are scaling factors.
In the fashion of equation (4), we can write the least squares inverse corresponding
to the system of equation (9):
| 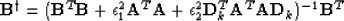 |
(10) |
Applying the downsampling operator 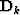 to the model vector attenuates high-frequency
components while boosting low-frequency components, thus we infer that the eigenvalue spectrum
of
to the model vector attenuates high-frequency
components while boosting low-frequency components, thus we infer that the eigenvalue spectrum
of 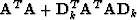 is better balanced than
that of
is better balanced than
that of 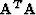 alone, which speeds convergence to a smooth model.
alone, which speeds convergence to a smooth model.
Claerbout (1999) presents a very similar multiscale methodology with one important difference:
the filters, not the data, are upscaled from one scale to the next. Crawley (2000)
applies this methodology to interpolating seismic data with nonstationary prediction error filters (PEF).
The PEF is more readily upscaled, since it is normally conceptualized as a dip annhilator,
and it annhilates the same dips at all scales. Unfortunately, other filters, like the Laplacian
finite difference filter used in this paper, do not have the self-similarity property of the PEF,
so explicitly expanding the filter is a dangerous proposition.





Next: Quadtree Pyramid Interpolation
Up: Background
Previous: Preconditioning
Stanford Exploration Project
9/5/2000
![\begin{displaymath}
\bf
\left[ \begin{array}
{c}
\bf B \ \epsilon_1 \bf A \...
...rray}
{c}
\bf d \ \bf 0 \
\bf 0
\end{array} \right].
\end{displaymath}](img26.gif)