




Next: Speed comparison
Up: Theory
Previous: Linking 1-D and 2-D
With the understanding that the 1-D FFT of a multi-dimensional signal
in helical coordinates is equivalent to the 2-D FFT, a natural
question to ask is: how does the helical wavenumber, kh, relate to
spatial wavenumbers, kx and ky?
The helical delay operator, Zh, is related to kh
through the equation,
| 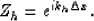 |
(8) |
In the discrete frequency domain this becomes
| 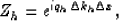 |
(9) |
where qh is the integer frequency index that lies in the range,
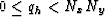 .
The uncertainty relationship,
.
The uncertainty relationship,
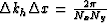 , allows this to be
simplified still further, leaving
, allows this to be
simplified still further, leaving
| 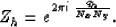 |
(10) |
If we find a form of qh in terms of Fourier indices,
qx and qy, that can be plugged into equation (10)
in order to satisfy equations (4)
and (5), this will provide the link between kh and
spatial wavenumbers, kx and ky.
The idea that x-axis wavenumbers will have a higher frequency than
y-axis wavenumbers, leads us to try a qh of the form,
Substituting this into equation (10) leads to
| 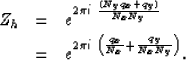 |
(12) |
| (13) |
Since qy is bounded by Ny, for large Nx the second term in
braces 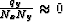 , and this
reduces to
, and this
reduces to
| 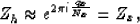 |
(14) |
which satisfies equation (4).
Substituting equation (11) into
equation (10), and raising it to the power of Nx leads
to:
| 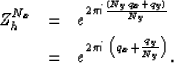 |
(15) |
| (16) |
Since qx is an integer, 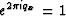 , and this reduces to
, and this reduces to
| 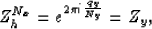 |
(17) |
which satisfies equation (5).
Equation (11), therefore, provides the link we are
looking for between qx, qy, and qh. It is interesting to
note that not only is there a one-to-one mapping between 1-D and 2-D
Fourier components, but equation (11) describes helical
boundaries in Fourier space: however, rather than wrapping around the
x-axis as it does in physical space, the helix wraps around the
ky-axis in Fourier space (Figure 2). This provides
the link that is missing in Figure 1, but shown in
Figure 3.
transp
Figure 2 Fourier dual of helical boundary
conditions is also helical boundary conditions with axis of helix
transposed.
|
| 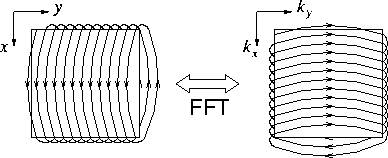 |

ill2
Figure 3 Relationship between 1-D and 2-D
convolution, FFT's and the helix, illustrating the Fourier dual of
helical boundary conditions.
|
| 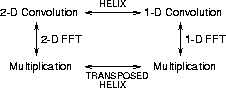 |

As with helical coordinates in physical space,
equation (11) can easily be inverted to yield
| ![\begin{eqnarray}
k_x & = & \Delta k_x \, q_x = \frac{2 \pi}{N_x \Delta x}
\left...
...y \Delta y}
\left(
q_h - N_y \left[ \frac{q_h}{N_y}\right]
\right)\end{eqnarray}](img24.gif) |
(18) |
| (19) |
where [x] denotes the integer part of x.





Next: Speed comparison
Up: Theory
Previous: Linking 1-D and 2-D
Stanford Exploration Project
9/5/2000
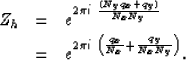
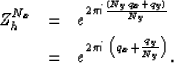

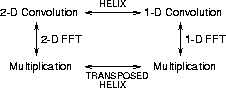
![\begin{eqnarray}
k_x & = & \Delta k_x \, q_x = \frac{2 \pi}{N_x \Delta x}
\left...
...y \Delta y}
\left(
q_h - N_y \left[ \frac{q_h}{N_y}\right]
\right)\end{eqnarray}](img24.gif)