The Fourier analogue of convolution is multiplication: to convolve a 2-D signal with a 2-D filter, take their 2-D Fourier transforms, multiply them together and return to the original domain. The relationship between 1-D and 2-D convolution, FFT's and the helix is illustrated in Figure 1. With helical boundary conditions, we can take advantage of the isomorphism described above, and perform multi-dimensional convolutions by wrapping multi-dimensional signals and filters onto a helix, taking their 1-D FFT's, multiplying them together, and then returning to the original domain.
If we can use 1-D FFT's to do 2-D convolutions, the isomorphism due to
the helical boundary conditions must extend into the Fourier domain.
In this paper, we explore the relationship between 1-D and
multi-dimensional FFT's in helical coordinate systems. Specifically
we demonstrate the link between the wavenumber vector, ![]() , in a
multi-dimensional system, and the wavenumber of a helical 1-D FFT,
kh.
, in a
multi-dimensional system, and the wavenumber of a helical 1-D FFT,
kh.
|
ill
Figure 1 Relationship between 1-D and 2-D convolution, FFT's and the helical boundary conditions. | 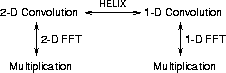 |