




Next: Sampling in time
Up: Prediction error filters
Previous: Scale invariance and filling
There are two steps. The first calculates a PEF and the
second calculates missing data values.
Both are linear least squares problems, which I solve
using conjugate gradients.
The first step we can write
| 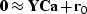 |
(18) |
where  is a vector containing the PEF coefficients,
is a vector containing the PEF coefficients,
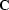 is a filter coefficient selector matrix,
and
is a filter coefficient selector matrix,
and 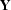 denotes convolution with the input data.
The coefficient selector
denotes convolution with the input data.
The coefficient selector 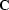 is like an identity
matrix, with a zero on the diagonal placed to prevent the
fixed 1 in the zero lag of the PEF from changing.
The
is like an identity
matrix, with a zero on the diagonal placed to prevent the
fixed 1 in the zero lag of the PEF from changing.
The  is a vector that holds the initial value
of the residual,
is a vector that holds the initial value
of the residual,  .If the unknown filter coefficients are given initial values
of zero, then
.If the unknown filter coefficients are given initial values
of zero, then  contains a copy of the input data.
contains a copy of the input data.
 makes up for the fact that the 1 in the zero
lag of the filter is not included in the convolution (it is
knocked out by
makes up for the fact that the 1 in the zero
lag of the filter is not included in the convolution (it is
knocked out by 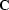 ).
).
The second step is almost the same, except we solve for
data values rather than filter coefficients,
so knowns and unknowns are reversed. We use
the entire filter, not leaving out the fixed 1,
so the 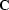 is gone, but we need a different selector
matrix, this time
to prevent the originally recorded data from changing.
Split the data into known and unknown parts with
an unknown data selector matrix
is gone, but we need a different selector
matrix, this time
to prevent the originally recorded data from changing.
Split the data into known and unknown parts with
an unknown data selector matrix  and
a known data selector matrix
and
a known data selector matrix 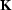 .Between the two of them they select every data sample
once:
.Between the two of them they select every data sample
once:  .Now to fill in the missing data values, solve
.Now to fill in the missing data values, solve
|  |
(19) |
| (20) |
| (21) |
 now denotes the convolution operator, and
the vector
now denotes the convolution operator, and
the vector  holds the data, with the selector
holds the data, with the selector  preventing any change to the known, originally recorded data values.
The
preventing any change to the known, originally recorded data values.
The  in interp is calculated just like
the
in interp is calculated just like
the  in pefest, except that now
the adjustable filter coefficients are presumably not zero.
Where before
in pefest, except that now
the adjustable filter coefficients are presumably not zero.
Where before  wound up holding a copy of the data
(assuming the adjustable filter coefficients start out zero),
here it holds the initial prediction error
wound up holding a copy of the data
(assuming the adjustable filter coefficients start out zero),
here it holds the initial prediction error  .
.
There is some wasted effort implied here.
There is no sense, for instance, in actually running the filter over
all those zero-valued missing traces in the PEF calculation step, so they
can be left out.





Next: Sampling in time
Up: Prediction error filters
Previous: Scale invariance and filling
Stanford Exploration Project
1/18/2001
![]() is gone, but we need a different selector
matrix, this time
to prevent the originally recorded data from changing.
Split the data into known and unknown parts with
an unknown data selector matrix
is gone, but we need a different selector
matrix, this time
to prevent the originally recorded data from changing.
Split the data into known and unknown parts with
an unknown data selector matrix ![]() and
a known data selector matrix
and
a known data selector matrix ![]() .Between the two of them they select every data sample
once:
.Between the two of them they select every data sample
once: ![]() .Now to fill in the missing data values, solve
.Now to fill in the missing data values, solve
