Next: Finite differences and spectral
Up: Fomel: Splines in tension
Previous: Introduction
The traditional minimum-curvature criterion implies seeking a
two-dimensional surface f(x,y) in region D, which corresponds to
the minimum of the Laplacian power:
| 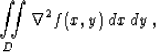 |
(1) |
where 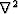 denotes the Laplacian operator:
denotes the Laplacian operator: 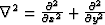 .
.
Alternatively, we can seek f(x,y) as the solution of the biharmonic
differential equation
| 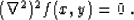 |
(2) |
Equation (2) corresponds to the normal system of equations
in the least-square optimization problem. Briggs (1974)
derives it directly from (1) with the help of Gauss's
theorem.
Formula (1) approximates the strain energy of a thin
elastic plate Timoshenko and Woinowsky-Krieger (1968). Taking tension into account modifies
both the energy formula (1) and the corresponding
equation (2). Smith and Wessel (1990) suggest the
following form of the modified equation:
| ![\begin{displaymath}
\left[(1-t) (\nabla^2)^2 - t (\nabla^2)\right] f(x,y) = 0\;,\end{displaymath}](img5.gif) |
(3) |
where the tension parameter t ranges from 0 to 1. Zero tension leads
to the biharmonic equation (2) and corresponds to the
minimum curvature construction. The case of t=1 corresponds to
infinite tension. Although infinite tension is physically impossible,
the resulting Laplace equation does have a physical interpretation of
a steady-state temperature distribution. An important property of
harmonic functions (solutions of the Laplace equation) is that they
cannot have local minima and maxima in the free regions. With respect
to interpolation, this means that, in the case of t=1, the
interpolation surface will be constrained to have its local extrema
only at the input locations.
To interpolate an irregular set of data values, fk at points
(xk,yk), we need to solve equation (3) under the
constraint
| 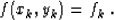 |
(4) |
An iterative solution of this problem can be greatly accelerated by
preconditioning Fomel et al. (1997); Fomel (1997). If
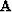 is the discrete filter representation of the differential
operator in equation (3), and we can find a minimum-phase
filter
is the discrete filter representation of the differential
operator in equation (3), and we can find a minimum-phase
filter 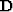 whose autocorrelation is equal to
whose autocorrelation is equal to 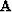 , then
an appropriate preconditioning operator is a recursive inverse
filtering with the filter
, then
an appropriate preconditioning operator is a recursive inverse
filtering with the filter 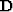 . Formulating the problem in
helical coordinates Claerbout (1998a,b)
allows us to perform both the spectral factorization of
. Formulating the problem in
helical coordinates Claerbout (1998a,b)
allows us to perform both the spectral factorization of 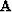 and
inverse filtering with
and
inverse filtering with 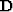 .
.





Next: Finite differences and spectral
Up: Fomel: Splines in tension
Previous: Introduction
Stanford Exploration Project
4/27/2000