 |
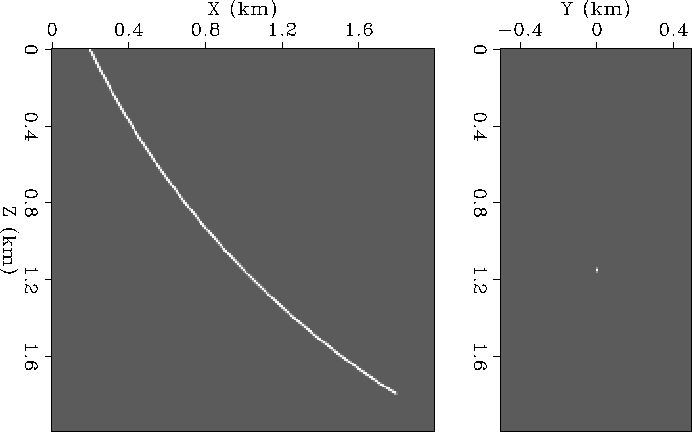
Figure 1 Traveltime sensitivity kernel for ray-based tomography in a linear v(z) model. The kernel is zero everywhere except along geometric ray-path. Right panel shows a cross-section at X=1 km.
Figure 1 shows the ray-theoretical traveltime sensitivity kernel: zero except along the geometric ray-path.
 |
Figures 2 and 3 show first Rytov traveltime sensitivity kernels for 30 Hz and 120 Hz wavelets respectively. The important features of these kernels are identical to the features of kernels that Marquering et al. (1999) obtained for teleseismic S-H wave scattering, and to Woodward's 1992 band-limited wave-paths. They have the appearance of a hollow banana: that is appearing as a banana if visualized in the plane of propagation, but as a doughnut on a cross-section perpendicular to the ray. Somewhat counter-intuitively, this suggests that traveltimes have zero sensitivity to small velocity perturbations along the geometric raypath. Fortunately, however, as the frequency of the seismic wavelet increases, the bananas become thinner, and approach the ray-theoretical kernels in the high-frequency limit. Parenthetically, it is also worth noticing that the width of the bananas increases with depth as the velocity (and seismic wavelength) increases.
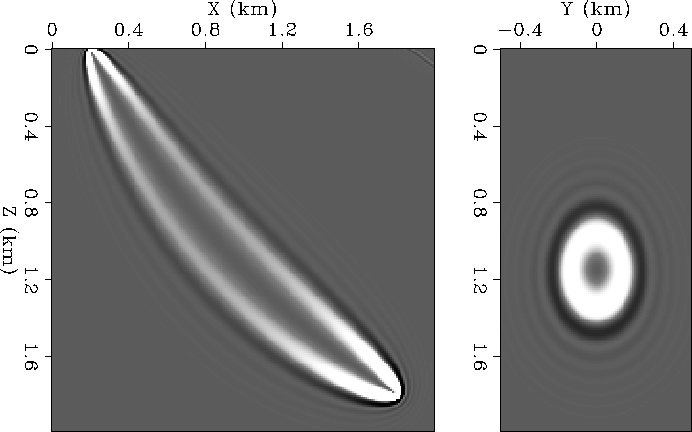 |
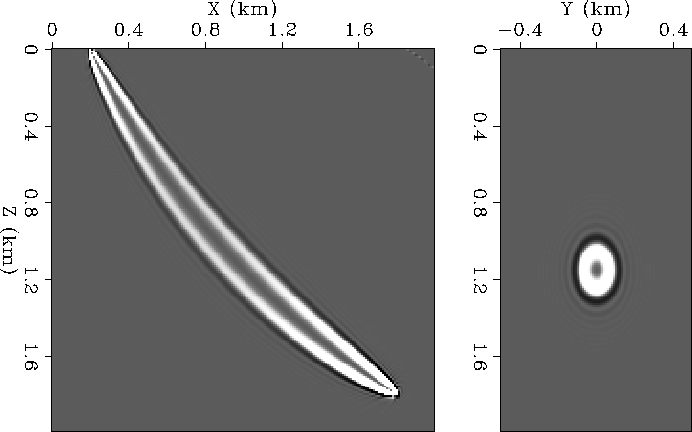 |
I do not show the first-Born kernels here, since, in appearance, they are identical to the Rytov kernels shown in Figures 2 and 3.