Discussion

Even if the parameter W estimated from equation (9) is optimal in the sense that it minimizes migration errors for the Stolt-stretch method, no single choice of W yields acceptable results for all times and all dips Beasley et al. (1988): some events are undermigrated, others overmigrated. Instead, the use of cascaded Stolt-stretch migration allows a reduction of the apparent dip perceived in each stage, since the migration velocity used is reduced to a fraction of the original model. A 20-stage cascade of migration with an algorithm accurate for dips up to $15^\circ$ can yield accurate results for events dipping up to $65^\circ$ Larner and Beasley (1987).

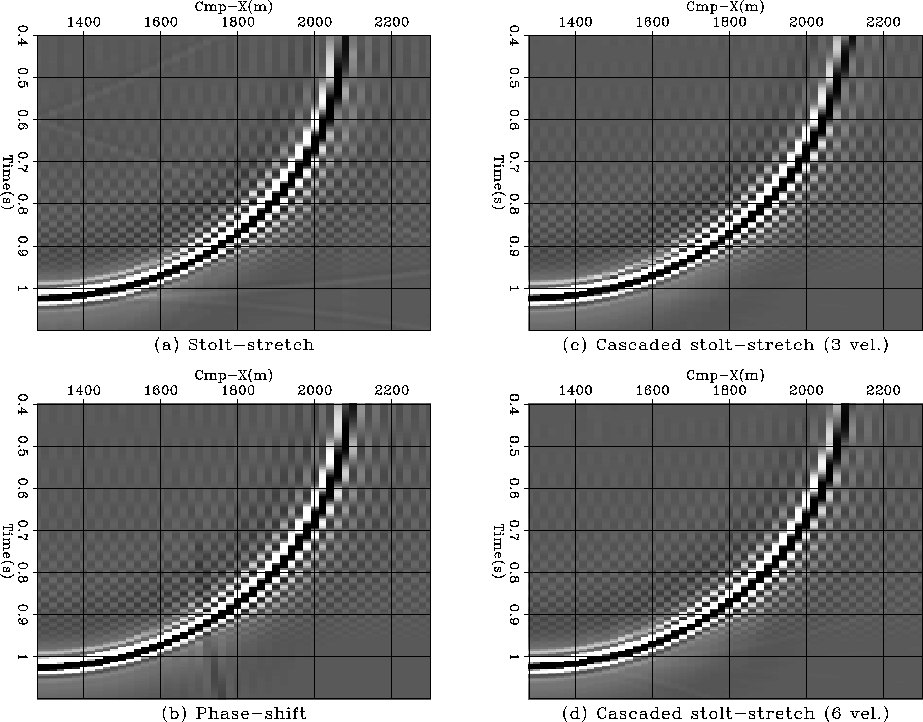
Figure 5 shows a close-up of the salt body region for all migration algorithms. The methods have a different accuracy with respect to steep dips. We notice a gradual improvement of the result from Stolt-stretch to phase-shift as we increase the number of velocities in the cascaded Stolt-stretch scheme. In theory, the migration errors in the cascaded approach can be made as small as desired by increasing the number of stages. At the limit, it corresponds to the velocity continuation concept Fomel (1996).

In our case, six stages were enough to obtain a result comparable to phase-shift. In their comparative study on time migration algorithms, Larner et al. 1989 have shown that four-stage cascaded f-k migration is accurate for dips up to $85^\circ$, which is almost comparable to phase-shift, accurate for all dips. It is worth noting the computational cost difference between the two: on our example, phase-shift migration is about 80 times more expensive than Stolt-stretch!

Another way to look at the problem is to compare the impulse responses of the different algorithms (Figure 6), generated using the same velocity model as before (Figure 4a). There is a kinematic difference in the impulse response of Stolt-stretch compared to phase-shift. While Gazdag's phase-shift honor ray bending in any v(z) model, Stolt-stretch is not that accurate. Both methods address non-hyperbolic moveout, but Stolt's stretching function is only designed to make the fitting curve look like an hyperbola close to the apex Levin (1983), and therefore induces residual migration errors. As seen in Figure 2a, Stolt-stretch result displays residual hyperbolic migration artifacts that are due to this fundamental kinematic difference. Cascading Stolt-stretch makes the impulse response of the migration converge towards the one of phase-shift.

 

dip-zoom
Figure 5 Zoom in the salt body area where steep dips are located. (a) Migration with the Stolt-stretch method. (b) Migration with the phase-shift method. (c) and (d) Migrations with the cascaded Stolt-stretch approach, using, respectively, 3 and 6 velocities.

Now that we are familiar with the role of W in the algorithm, a word should be said about v₀, which is the second arbitrary parameter of the method. As introduced in equation (4), v₀ controls the length of the stretch. In theory, the migration result does not depend on the selected value, since the time stretch is undone after Stolt migration. However, in practice, high values of v₀ can yield an image with interpolation artifacts. In contrast, low values of v₀ yield a significantly stretched time axis, thus the inverse operation may lose information unless the data has been padded with enough zeroes. The cascaded scheme is particularly sensitive to such problems. As a tradeoff between values that are too high or too small, we used the mean of the velocity model extrema for v₀.

Another technical aspect, the division by the Jacobian in equation (2), usually induces high amplitude artifacts for waves close to being evanescent, unless a threshold is introduced. Similarly, evanescent waves need to be scaled down to prevent migration artifacts. We used a simple linear weighting.

 

imp-mig
Figure 6 Impulses responses of the different operators. (a) Stolt-stretch. (b) Phase-shift. (c) and (d) Cascaded Stolt-stretch, with 3 and 6 velocities, respectively.