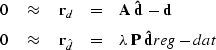
In order to compute stable solutions to ill-conditioned systems it is often necessary to apply regularization methods. Claerbout 1997 writes: `` In geophysical fitting we generally have two goals, the first being data ``fitting'' and the second being the ``damping'' or regularization goal''. One way to achieve such objective is to augment the problem with a second regression that adds assumptions about the model (e.g. roughness, smoothness, curvature, energy in one dip, etc...).
For the data-space inverse, one now solves the problem:
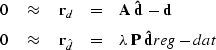 |
(59) | |
The solution ![]() represents an
equalized data vector that is unevenly sampled. I chose the penalty
operator,
represents an
equalized data vector that is unevenly sampled. I chose the penalty
operator, ![]() , to be the identity matrix.
This is the standard Tikhonov regularization
where the solution
, to be the identity matrix.
This is the standard Tikhonov regularization
where the solution ![]() solves the problem:
solves the problem:
| (60) |
Similar to the data-space solution, to regularize the model-space inverse one seeks a solution to the system of regressions:
| (61) | ||
| (62) |
Since the model ![]() is regularly sampled, I chose
is regularly sampled, I chose ![]() to be
the Laplacian operator, which represents differentiation in the midpoint-space.
The parameter
to be
the Laplacian operator, which represents differentiation in the midpoint-space.
The parameter ![]() controls
the smoothness of the solution and is again
an estimate of the smallest resolved singular value of
controls
the smoothness of the solution and is again
an estimate of the smallest resolved singular value of ![]() .At the time of writing the dissertation, I didn't investigate a
robust strategy for estimating
.At the time of writing the dissertation, I didn't investigate a
robust strategy for estimating ![]() . However, by processing
a single frequency (e.g the dominant frequency of the survey), I was
able to iteratively guess a good estimate for
. However, by processing
a single frequency (e.g the dominant frequency of the survey), I was
able to iteratively guess a good estimate for ![]() . Ideally, one
might assume a different value for
. Ideally, one
might assume a different value for ![]() should be used for
each frequency inversion. Results showed that a single good
estimate of
should be used for
each frequency inversion. Results showed that a single good
estimate of ![]() produced
a reasonably smooth solution while still
preserving the high frequency components of the reflectivity function.
produced
a reasonably smooth solution while still
preserving the high frequency components of the reflectivity function.