Data and Model preconditioning

Proper balancing of the matrix ${\bf L}$ can be achieved by scaling in both data space and model space. However, applying either diagonal transformation ensures common magnitude of the elements of ${\bf L}$.The diagonal operators ${\bf R^{-1}}$ and ${\bf C^{-1}}$have physical units inverse to $\bold L$. Therefore applying both of them can only result into an ill-conditioned system where the matrix $\bold L$ has the inverse of its original units.

I propose a new formulation for balancing the matrix ${\bf L}$ by scaling both its rows and columns. The new formulation introduces a new parameter n, and solves the system

$$\bold R^{-n} \bold d = \bold R^{-n} \bold L \bold C^{n-1} \bold x. \EQNLABEL{prec-both}$$ (58)

where $0 \leq n \leq 1$.

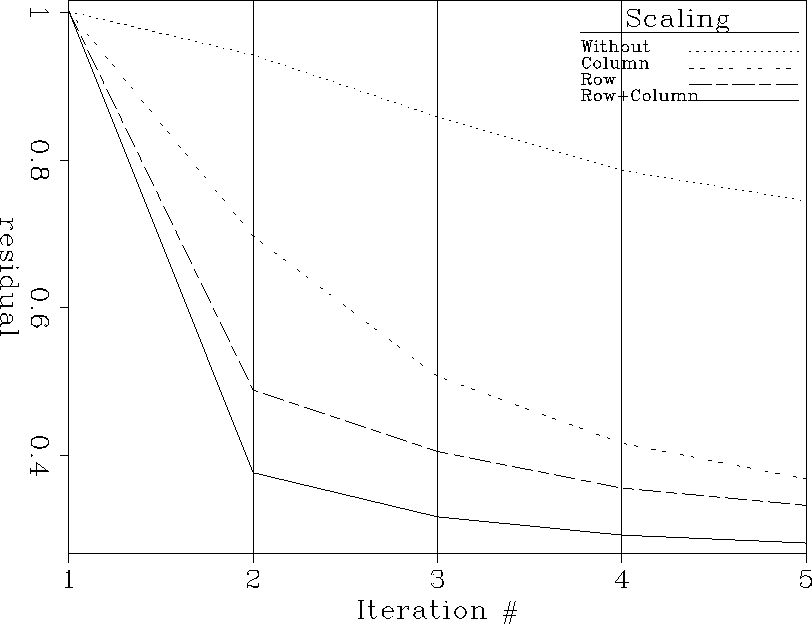
For n=0, the system prec-both reduces to the case of column scaling, whereas for n=1 it reduces to applying row scaling in the data space. As Figure residual shows, the diagonal transformation has proved to be a suitable preconditioner for the linear system. A good solution was obtained after 5 to 8 iterations of conjugate gradient solver. The column scaling improved the convergence of the iterative solution and resulted into faster convergence than the row scaling. A better convergence was achieved by applying a scaling to both the data space and model space for a value of n=1/2. An optimal value of n should probably depend on wether the system to be solved is mostly over-determined or under-determined. This should remain an interesting subject of investigation.

 

residual
Figure 1 Convergence of the model-space solution for one frequency inversion using different preconditioners.