Integral implementation of AMO

This section discusses practical issues for a cost-effective implementation of AMO as an integral operator in the time-space domain. The main challenge is to take advantage of the limited aperture for the integration to save computational costs while avoiding operator aliasing. For small azimuthal rotations, the saddle describing the AMO impulse response has a strong curvature that requires special handling of operator antialiasing. The trick is to perform the spatial integration in a transformed coordinate system where the AMO surface becomes invariant with respect to the amount of azimuth rotation and offset continuation. The appropriate midpoint-coordinate transformation is described by the following chain of transformations Fomel and Biondi (1995b):

$$\left[ \begin{array} {c} \xi_1\\ \xi_2\\ \end{array}... ..._x \\ \Delta m_y \end{array} \right]\;, \EQNLABEL{transform}$$ (5)

where $\xi_1$, and $\xi_2$ are the transformed midpoint coordinates. Figure amonewcoord shows a schematic of the relationship between the input and output offset vectors ${\bf h}_{1}$ and ${\bf h}_{2}$, and the transformed midpoint-coordinate unit vectors ${\bf \xi}_1$and ${\bf \xi}_2$. The right matrix represents a space-invariant rotational squeezing of the coordinate, while the left matrix is a simple rescaling of the axes by a factor dependent on the azimuth rotation $\Delta \theta$ and the length of the offset vectors.

 

amonewcoord
Figure 4 The geometric relationship between the unit vectors ${\bf \xi}_1$ and ${\bf \xi}_2$of the transformed midpoint-coordinate axes, and the input offset ${\bf h}_{1}$ and the output offset ${\bf h}_{2}$.

In this new coordinate system, the kinematics of AMO are described by the following simple relationship between the input time t₁ and the output time t₂

$$t_2\left(\xi_1, \xi_2\right)=t_1\,\sqrt{\frac{1-{\xi_2}^2}{1-{\xi_1}^2}}\;, \EQNLABEL{traveltime}$$ (6)

and the amplitudes (based on Zhang-Black amplitudes for DMO) are described by the following equation

$$A\left(\xi_1, \xi_2\right)=\frac{t_2 \left\vert\omega_2\righ... ...i_1}^2\right)\left(1-{\xi_2}^2\right)}}\;. \EQNLABEL{amplitude}$$ (7)

which takes into account the Jacobian factor introduced by the coordinate transformation.

To avoid operator aliasing, one should apply a low-pass filter whose bandwidth varies spatially along the operator and is a function of the local time dips of the operator. The time dips can be computed analytically according to the following equations:

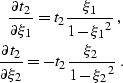$$\begin{eqnarray} \frac{\partial t_2}{\partial \xi_1}=t_2\frac{\xi_1}{1-{\xi_1}^2... ...rac{\partial t_2}{\partial \xi_2}=-t_2\frac{\xi_2}{1-{\xi_2}^2}\;.\end{eqnarray}$$ (8) (9)

Finally, and taking into account the dependency of the AMO aperture on velocity, the maximum output time can be evaluated for a given minimum propagation velocity V_min as

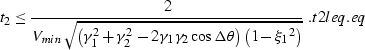$$t_2 \leq \frac{2}{V_{min}\sqrt{\left(\gamma_1^2 + \gamma_2^2... ... \theta\right)\left(1-{\xi_1}^2\right)}}\;. \EQNLABEL{t2leq.eq}$$ (10)

where $\gamma_1$ and $\gamma_2$ are given by

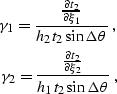$$\begin{eqnarray} \gamma_1=\frac{\frac{\partial t_2}{\partial \xi_1}}{h_{2}t_2\si... ...\frac{\partial t_2}{\partial \xi_2}}{h_{1}t_2\sin\Delta \theta}\;,\end{eqnarray}$$ (11) (12)

To avoid truncation artifacts, a tapering function should be applied to the edges of the operator aperture.