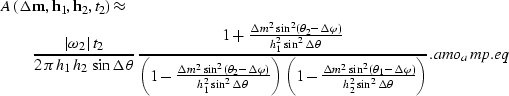
While the kinematics of AMO are independent of its derivation, the amplitude term varies according to the derivation. In the next chapter I present detailed derivations for a true-amplitude function for the AMO operator. In short, the weights are based on the cascade of an amplitude preserving DMO with its asymptotic ``true-inverse'' Chemingui and Biondi (1995). The choice of Zhang-Black's Jacobian yields the following expression for the amplitude term:
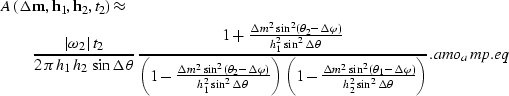 |
||
| (4) |
The frequency term ![]() enters as
multiplicative factor in the expression for AMO amplitudes.
This term can be applied
to the output data
in the time domain
by cascading a causal half-differentiator with
an anti-causal half-differentiator.
enters as
multiplicative factor in the expression for AMO amplitudes.
This term can be applied
to the output data
in the time domain
by cascading a causal half-differentiator with
an anti-causal half-differentiator.