Helix low-cut filter

I check the effects of adjustable parameters k₀, n_a and $\rho$ on roughened images. The quantitative analysis of the effects on the filter spectrum is provided in appendix A.

When comparing the effects of k₀ and n_a, I set $\rho=1$ to make sure the filters have the same zero-frequency response. Figure 3 shows the Bay Area map created with different k₀. As k₀ increases, more low-frequency components were removed and the detailed structure turns out to be the main focus of the map. This indicates the cut-off frequency increases as k₀ increases. In other words, k₀ governs the cut-off frequency. When k₀ remains the same, filters with different n_a can create very similar results if the zero-frequency response is the same by adjusting $\rho$, as shown in the middle and bottom plots in Figure 4. As expected, $\rho$ controls the zero-frequency response. The larger $\rho$ leads to higher contrast, as shown in the top and middle plots in Figure 4.

 

bay-lct-k-a16r1
Figure 3 Bay Area maps roughened by helix low-cut filters with different k₀. The top is k₀=0.1, the middle is k₀=0.3, the bottom is k₀=0.5. n_a=16, $\rho=1$.As k₀ increases, the cut-off frequency increases.

 

bay-lct-ar-k3
Figure 4 Bay Area maps roughened by helix low-cut filters with different filter length. The top is n_a=8 and $\rho=0$, the middle is n_a=16 and $\rho=1$, the bottom is n_a=32. k₀=0.3, $\rho=1$. k₀=0.3. As $\rho$ increases, the zero-frequency response decreases. When the zero-frequency response remains the same, the difference of n_a does not affect results.

Among the three adjustable parameters, n_a is the least important one because the long filter can be replaced with a short one by adjusting $\rho$.k₀ controls the cut-off frequency and $\rho$ controls the zero-frequency response. It is hard to tell which one is more important if I use only this information. From the quantitative analysis, I know k₀ affects zero-frequency response significantly, but $\rho$ does not have such an influence on cut-off frequency. So k₀ is the most important parameter.

For the enhanced helix low-cut filter, it is very reasonable to choose parameter k₀ first, then $\rho$ and n_a.

When roughening the image with the helix low-cut filter, the key point is to choose the cut-off frequency f₀ or the adjustable parameter k₀. My suggestion is that if the lowest frequency component to be preserved is f_L, k₀ should be  

$$k_0 = \frac{2}{3} f_L$$ (5)

Therefore, the frequency far below f_L would be cut off completely, and the component near f_L would not be affected too much.

Since the short filter is made equivalent to the long filter by adjusting $\rho$, I suggest the use of $n_a \approx 16$ based on the balance of computation costs and symmetric features.

With k₀ and n_a determined, I can find $\rho$ according to Equation (13)  

$$\rho = 1-\frac{I_0 n_a k_0}{0.82}$$ (6)

If $\rho=1$, the zero-frequency is removed completely and leads to the highest contrast in the roughened image.

Figure 5 consists of three maps of the Bay Area. The top portion is a topographic map of the Bay Area. The bottom plot is the preferred result. From one slice of the Bay Area topographic map, I know one main low frequency component is about 0.4. So I chose k₀ = 0.3 to remove the lower frequency. I chose n_a = 16. In order to obtain the highest contrast, I chose $\rho=1$. The middle one is the reference plot with k₀ = 0.1, n_a =16 and $\rho=1$. I notice that the bottom plot removes more low frequency components than the middle one and has clearer details, as predicted by the theory.

 

bay-lct-res
Figure 5 Bay Area maps. The top is the topographic map; the other two are roughened with helix low-cut filter. The middle is k₀ = 0.1; and the bottom is k₀ = 0.3. n_a = 16, $\rho=1$.

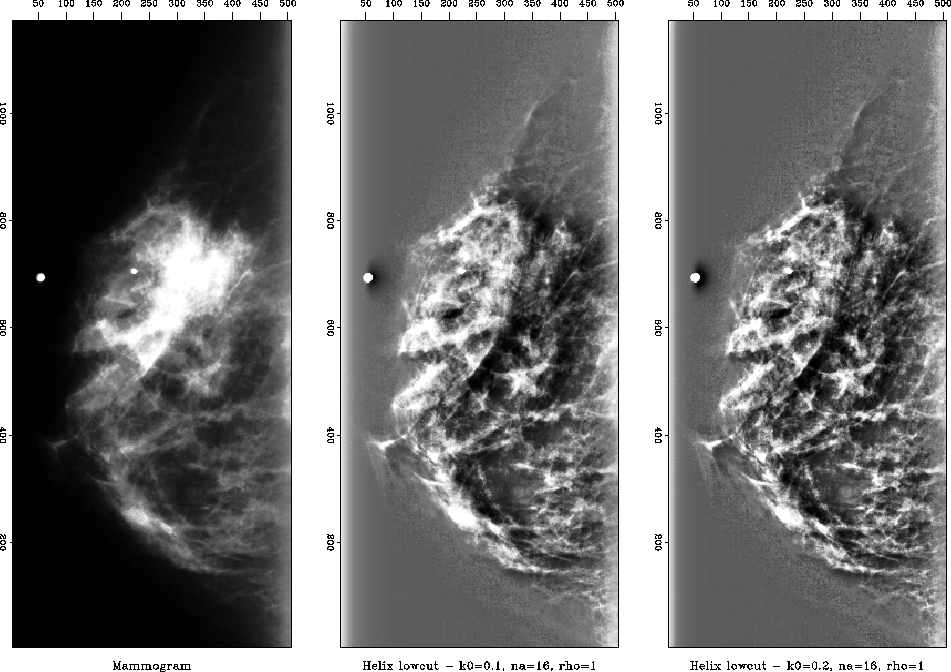
Figure 6 consists of a normal mammogram and the roughened images. The main low frequency component of the mammogram slice is about 0.3, so I choose k₀ = 0.2 in the right plot as the preferred result, and use k₀ = 0.1 in the middle as reference. I use $\rho=1$ to achieve the highest contrast.

 

mam-lct-res
Figure 6 Mammogram (medical X-ray). The left figure is the origin map; the right two are filtered with helix low-cut filter. n_a =16, $\rho=1$, the middle is k₀=0.1, the right is k₀=0.2.