Figure 9 is the zero-frequency response and
cut-off
frequency of a 100-point low-cut filter for different k0 when ![]() .I find that cut-off frequency f0 is almost the same as k0.
.I find that cut-off frequency f0 is almost the same as k0.
| |
(9) |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) very well.
In Equation (2), if I set k = k0, the expression
of
) very well.
In Equation (2), if I set k = k0, the expression
of The difference of the cut-off frequencies at various azimuths is very small when k0 > 0.1 and can be ignored. For k0 < 0.1, the difference is obvious.
In Figure 9, the zero-frequency
response decreases as k0 increases.
For ![]() and k0>0.03,
and k0>0.03, ![]() , the empirical
relationship between the
zero-frequency response of 100-point and k0 is
, the empirical
relationship between the
zero-frequency response of 100-point and k0 is
| |
(10) |
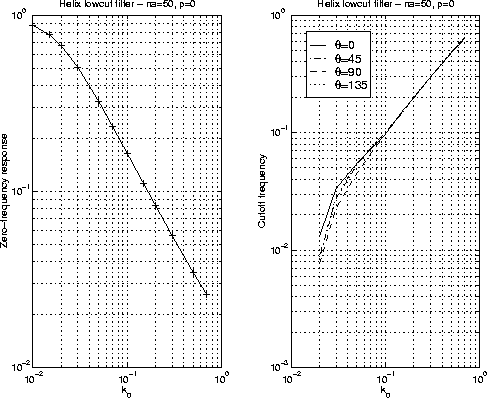 |
Figure 9 The zero-frequency response and cut-off frequency of the helix low-cut filter with na =50,
Figure 10 shows the effect of na on helix low-cut
filter when k0 = 0.3 and ![]() .For small na, the numerical anisotropy is very strong. Although the
mean value of the cut-off frequency remains the same, the azimuthal
difference becomes larger when na becomes smaller.
The zero-frequency response increases
as na decreases, and when k0 =0.3 and
.For small na, the numerical anisotropy is very strong. Although the
mean value of the cut-off frequency remains the same, the azimuthal
difference becomes larger when na becomes smaller.
The zero-frequency response increases
as na decreases, and when k0 =0.3 and ![]() , the empirical
expression is
, the empirical
expression is
| |
(11) |
 |
Figure 10 The zero-frequency response and cut-off frequency of the helix low-cut filter with k0 = 0.3,
![]() directly controls the zero-frequency response and affects the
cut-off frequency as well.
Figure 11 shows the cut-off frequency of the
100-point helix low-cut filter as the function of k0 when
directly controls the zero-frequency response and affects the
cut-off frequency as well.
Figure 11 shows the cut-off frequency of the
100-point helix low-cut filter as the function of k0 when ![]() and
and ![]() .For larger
.For larger ![]() , the numerical anisotropy is stronger, especially
when k0 is small. Compared with Figure 9, the cut-off
frequency at small k0 increases slightly with
, the numerical anisotropy is stronger, especially
when k0 is small. Compared with Figure 9, the cut-off
frequency at small k0 increases slightly with ![]() .
.
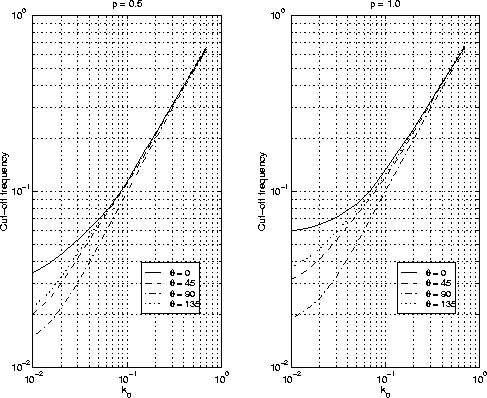 |
Figure 11 The zero-frequency response and cut-off frequency of helix low-cut filter.
Based on the proceeding analysis, I can derive the composed effects of the adjustable parameters on the helix low-cut filter.
The cut-off frequency is mainly governed by k0.
| |
(12) |
The zero-frequency response R0 is under the direct control of ![]() and
influenced by na and k0.
If I assume that the influences of na
and k0 are independent, the empirical expression of R0 would be
and
influenced by na and k0.
If I assume that the influences of na
and k0 are independent, the empirical expression of R0 would be
| |
(13) |