




Next: Helix low-cut filter
Up: Quantitative effect of the
Previous: Quantitative effect of the
For the helix derivative filter, the response is nearly a linear function
of 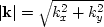 and does not have the ``cut-off
frequency''. The main feature here is the zero-frequency response.
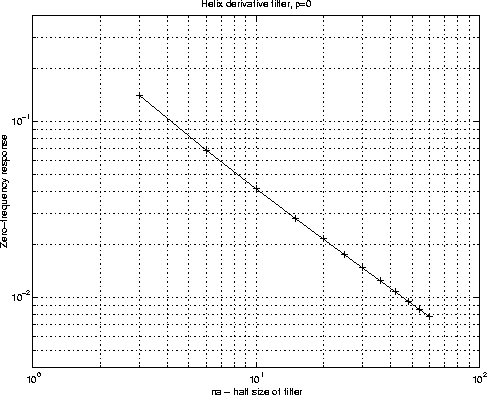
Figure 8 shows the zero-frequency response R0
as the function of filter length when
and does not have the ``cut-off
frequency''. The main feature here is the zero-frequency response.
Figure 8 shows the zero-frequency response R0
as the function of filter length when 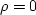 . na is the half
size of the filter. I find that R0 decreases as na increases
and
. na is the half
size of the filter. I find that R0 decreases as na increases
and 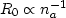 . The empirical relationship between R0
and na is
. The empirical relationship between R0
and na is
| 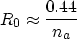 |
(7) |
R0 is the sum of the helix filter's coefficients, so when 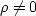 ,according to Equation (3), the
zero-frequency response is
,according to Equation (3), the
zero-frequency response is
| 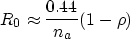 |
(8) |
drv-r0f-ar0
Figure 8 The zero-frequency response of helix
derivative filter when 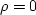 . The approximate zero-frequency response
is
. The approximate zero-frequency response
is 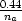 .
.





The zero-frequency response of the enhanced helix derivative filter is
controlled
by both na and 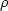 , I can compute the approximate value of R0
using Equation (8).
, I can compute the approximate value of R0
using Equation (8).





Next: Helix low-cut filter
Up: Quantitative effect of the
Previous: Quantitative effect of the
Stanford Exploration Project
4/20/1999
![]() , I can compute the approximate value of R0
using Equation (8).
, I can compute the approximate value of R0
using Equation (8).