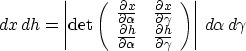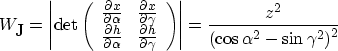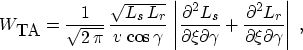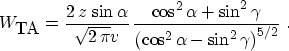Next: Examples
Up: Fomel & Prucha: Angle-gather
Previous: Traveltime considerations
One simple approach to amplitude weighting for angle-gather migration
is based again on Cheops' pyramid considerations. Stacking along the
pyramid in the data space is a double integration in midpoint and
offset coordinates. Angle-gather migration implies the change of
coordinates from 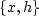 to
to 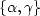 . The change of
coordinates leads to weighting the integrand by the following Jacobian
transformation:
. The change of
coordinates leads to weighting the integrand by the following Jacobian
transformation:
| 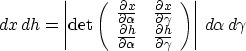 |
(11) |
Substituting formulas (5) and (6) into equation
(11) gives us the following analytical expression for the
Jacobian weighting:
| 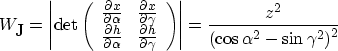 |
(12) |
Weighting (12) should be applied in addition to the
weighting used in common-offset migration. By analyzing formula
(12), we can see that the weight increases with the
reflector depth and peaks where the angles  and
and 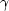 approach condition (10).
approach condition (10).
The Jacobian weighting approach, however, does not provide physically
meaningful amplitudes, when migrated angle gathers are considered
individually. In order to obtain a physically meaningful amplitude, we
can turn to the asymptotic theory of true-amplitude migration
Goldin (1992); Schleicher et al. (1993); Tygel et al. (1994). The true-amplitude weighting provides an
asymptotic high-frequency amplitude proportional to the reflection
coefficient, with the wave propagation (geometric spreading) effects
removed. The generic true-amplitude weighting formula
Fomel (1996b) transforms in the case of 2-D angle-gather
time migration to the form:
| 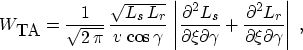 |
(13) |
where Ls and Lr are the ray lengths from the reflector point to
the source and the receiver respectively. After some heavy algebra,
the true-amplitude expression takes the form
| 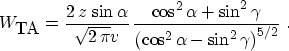 |
(14) |
Under the constant-velocity assumption and in high-frequency
asymptotic, this weighting produces an output, proportional to the
reflection coefficient, when applied for creating an angle gather with
the reflection angle 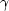 . Despite the strong assumptions behind
this approach, it might be useful in practice for post-migration
amplitude-versus-angle studies. Unlike the conventional common-offset
migration, the angle-gather approach produces the output directly in
reflection angle coordinates. One can use the generic true-amplitude
theory Fomel (1996b) for extending formula (14)
to the 3-D and 2.5-D cases.
. Despite the strong assumptions behind
this approach, it might be useful in practice for post-migration
amplitude-versus-angle studies. Unlike the conventional common-offset
migration, the angle-gather approach produces the output directly in
reflection angle coordinates. One can use the generic true-amplitude
theory Fomel (1996b) for extending formula (14)
to the 3-D and 2.5-D cases.





Next: Examples
Up: Fomel & Prucha: Angle-gather
Previous: Traveltime considerations
Stanford Exploration Project
4/20/1999
![]() to
to ![]() . The change of
coordinates leads to weighting the integrand by the following Jacobian
transformation:
. The change of
coordinates leads to weighting the integrand by the following Jacobian
transformation: