![]()
![]()
![]()
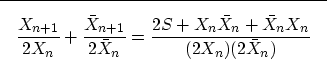 |
(9) |
| |
(10) |
In an analogous way, we can take the general relation from Table 3
![]()
![]()
![]()
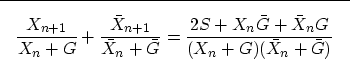 |
(11) |
Equation (11) represents our general formula for spectral factorization. If we consider the particular case when G is Xn, we obtain equation (10), which we have shown to be equivalent to the Wilson-Burg formula.
From the computational standpoint, our equation is more expensive than the Wilson-Burg because it requires two more convolutions on the numerator of the right-hand side. However, our equation offers more flexibility in the convergence rate. If we try to achieve a quick convergence, we can take G to be Xn and get the Wilson-Burg equation. On the other hand, if we worry about the stability, especially when some of the roots of the auto-correlation function are close to the unit circle, and we fear losing the minimum-phase property of the factors, we can take G to be some damping function, more tolerant of numerical errors.
Moreover, by using the Equation (11), we can achieve fast convergence in cases when the auto-correlations we are factorizing have a very similar form, for example, in nonstationary filtering. In such cases, the solution at the preceding step can be used as the G function in the new factorization. Since G is already very close to the solution, the convergence is likely to occur quite fast.