Next: Conclusions
Up: Sava: Residual migration
Previous: 3-D Residual Stolt Migration
In this section, I present two 2-D post-stack synthetic examples,
shown in Figures 2 and 3, to
prove the applicability of the equations derived in the preceding
sections.
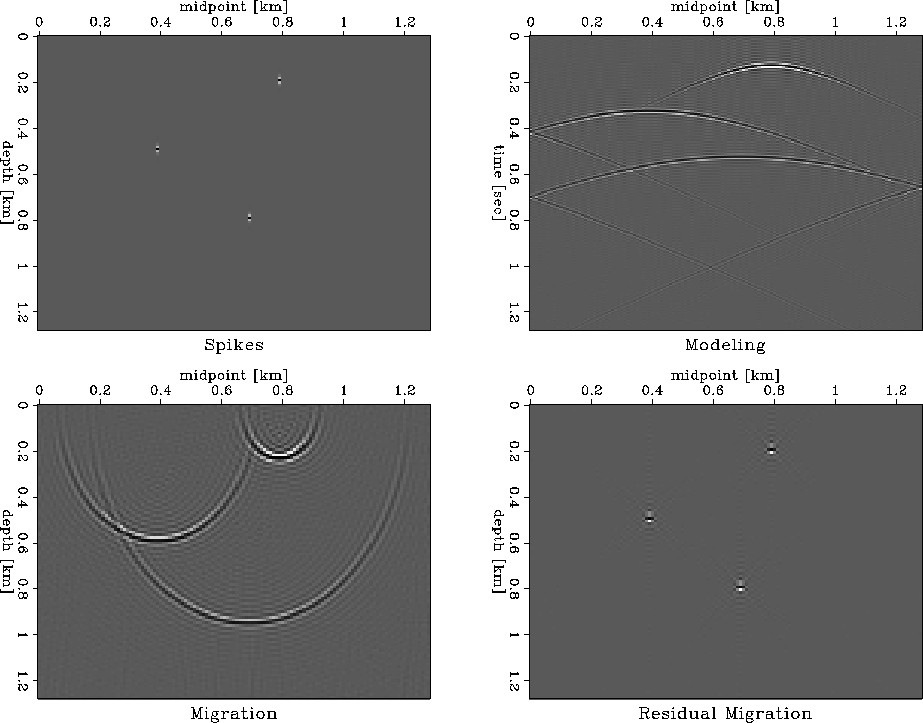
In the first example, the input is a set of three spikes. Initially, I
do forward modeling with a velocity of vm=3.0 km/s. Next, I do Stolt
migration with a velocity of v0=3.6 km/s, and residual Stolt
migration with a ratio v0/vm=1.2 (Figure 2). I then
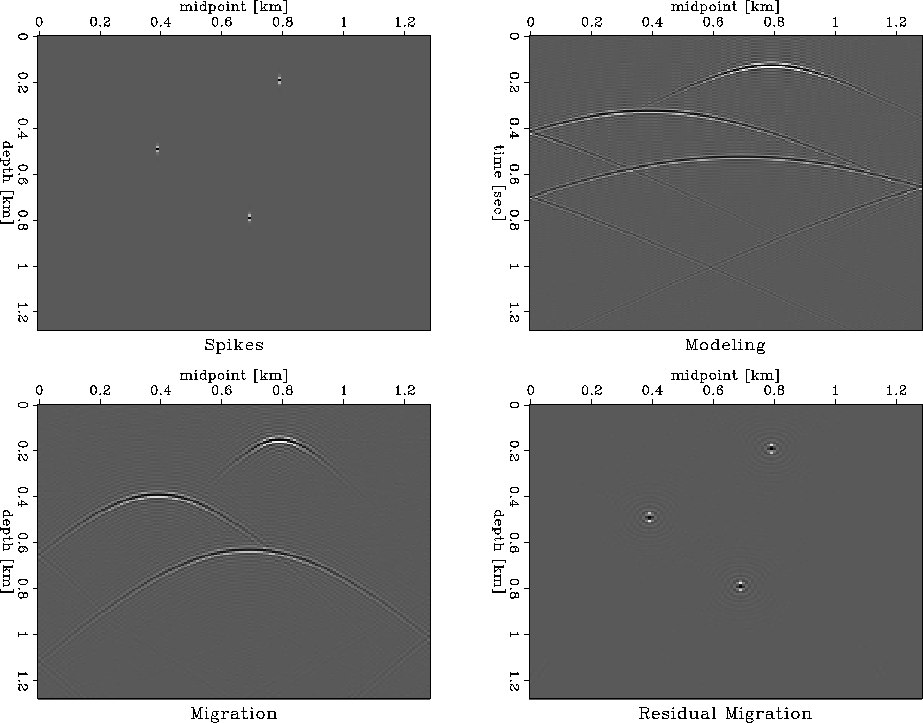
take the same input and perform Stolt migration with a velocity of
v0=2.4 km/s, followed by residual Stolt migration with a ratio
v0/vm=0.8 (Figure 3). In both cases, the data are
correctly collapsed at the location of the original spikes. Residual
migration can be done without knowing the absolute values of the
velocity.
posp
Figure 2
Top left: input data.
Top right: Stolt forward modeling with the correct velocity vm=3.0 km/s.
Bottom left: Stolt migration with an incorrect velocity of v0=3.6 km/s.
Bottom right: Stolt residual migration with the ratio v0/vm=1.2.




 posm
posm
Figure 3
Top left: input data.
Top right: Stolt forward modeling with the correct velocity vm=3.0 km/s.
Bottom left: Stolt migration with an incorrect velocity of v0=2.4 km/s.
Bottom right: Stolt residual migration with the ratio v0/vm=0.8.





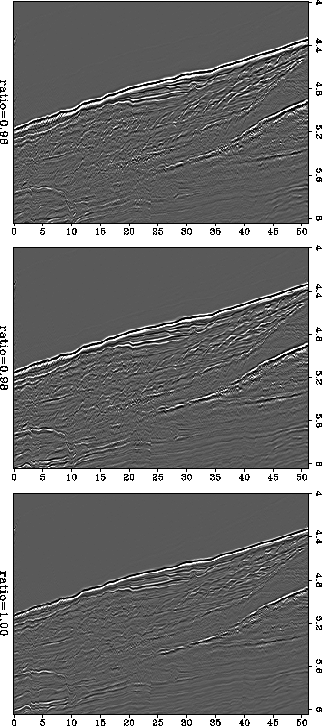
In the next example, shown in Figure 4, I apply
the same methodology to a real dataset Ecker (1998).
All three panels are the result of residual migration as described
in the preceding theory sections.
The corresponding ratios are 0.96 for the top panel, 0.98
for middle panel, and 1.00 for the bottom panel.
Residual migration with ratio=1.0 is equivalent to no residual
migration at all. It is apparent that different images are focused
better in one region or another, although the image corresponding to
the ratio 0.98 seems to have the highest overall energy. We can use
such an observation to obtain an image that has the best focusing in
all the regions. This can be achieved by doing residual migration for
a range of velocity ratios, and then interpolating the image that is best
focused everywhere. One possible application is in wave-equation
migration velocity analysis, where we can improve the focusing of a
depth-migrated dataset by residual migration, without making any
assumption about the original velocity distribution
Biondi and Sava (1999).
hydrates
Figure 4 Images obtained after
residual migration. Ratio = 1.00 means no residual
migration. Different images are focused better in different
regions. The image corresponding to ratio = 0.98 seems to have the
best focusing.










Next: Conclusions
Up: Sava: Residual migration
Previous: 3-D Residual Stolt Migration
Stanford Exploration Project
6/30/1999