




Next: Conclusions
Up: Rickett & Fomel: Second-order
Previous: Accuracy
The leading term in the computational cost of the fast marching
algorithm comes from the first step:
choosing the point on the wavefront with the smallest traveltime.
Consequently, the cost should not depend strongly on the order of the
finite-difference stencil, but rather the sort algorithm used.
Heap sorting has a cost of 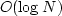 , and so in principle, with this
algorithm, the fast marching method has a cost of .
, and so in principle, with this
algorithm, the fast marching method has a cost of .
The left panel of Figure 4 shows a plot of CPU time
against N for the same models as Figure 2.
The time shown is elapsed (wall clock) time on a 300 MHz Pentium II.
For the largest model computed here, the second-order code takes 11%
longer to run than the first-order code, and this percentage decreases
as N increases.
Because 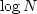 grows slowly compared to N, the plot of CPU time
against N is dominated by the linear term. The right panel in
Figure 4 addresses this issue by showing CPU time
divided by N versus N. On this graph, the
grows slowly compared to N, the plot of CPU time
against N is dominated by the linear term. The right panel in
Figure 4 addresses this issue by showing CPU time
divided by N versus N. On this graph, the 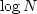 behaviour is
clearly visible.
behaviour is
clearly visible.
times
Figure 4 Elapsed CPU time vs. the number of grid
points, N, for first-order (solid line) and second order (dashed
line) eikonal solvers. Left panel shows CPU time vs N. Right
panel shows CPU time/N vs N.










Next: Conclusions
Up: Rickett & Fomel: Second-order
Previous: Accuracy
Stanford Exploration Project
4/20/1999
![]() grows slowly compared to N, the plot of CPU time
against N is dominated by the linear term. The right panel in
Figure 4 addresses this issue by showing CPU time
divided by N versus N. On this graph, the
grows slowly compared to N, the plot of CPU time
against N is dominated by the linear term. The right panel in
Figure 4 addresses this issue by showing CPU time
divided by N versus N. On this graph, the ![]() behaviour is
clearly visible.
behaviour is
clearly visible.
