Next: Computational cost
Up: Rickett & Fomel: Second-order
Previous: Fast marching and the
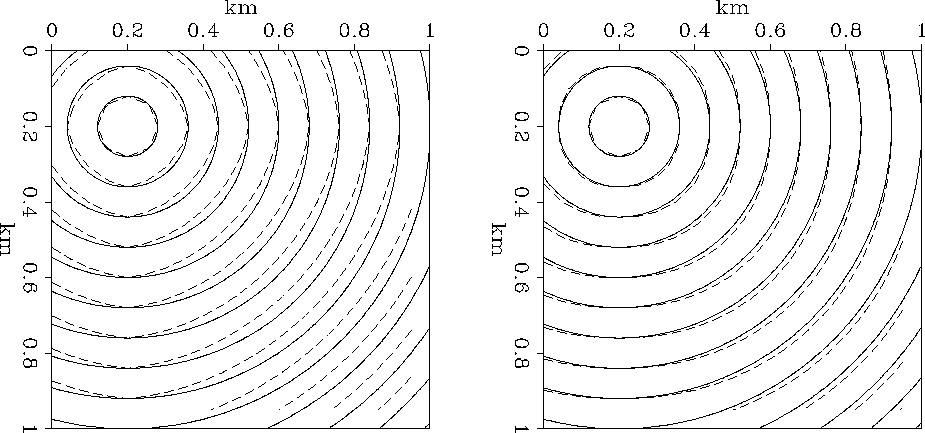
Figure 1 shows traveltime
contour maps computed with the first and second-order fast marching
methods on a sparse (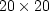 ) grid.
The large errors for waves propagating at 45
) grid.
The large errors for waves propagating at 45 to the grid are
visibly reduced by the second-order formulation.
circles
to the grid are
visibly reduced by the second-order formulation.
circles
Figure 1 Traveltime contours in a constant
velocity medium. The solid line shows the exact result. The dashed
line shows the first-order (left panel) and second-order (right panel)
fast marching results, calculated on a 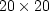 grid.
grid.





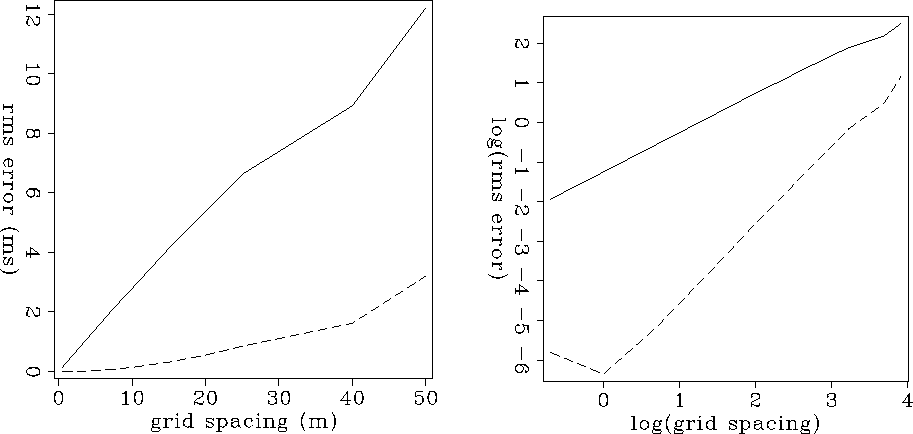
Figure 2 shows the average error as a function of grid
spacing for the first and second-order solvers. Not only is the
second-order formulation more accurate at large grid spacing, but its
accuracy increases more rapidly as grid spacing decreases.
Theory predicts the 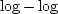 plots of average error against
grid spacing to be a linear function with gradient of one for
first-order methods, and two for second order methods.
In practice, the fast marching results come very close to these
criteria up to the limits of machine precision.
Figure 2 demonstrates the superiority of the
second-order fast marching formulation.
plots of average error against
grid spacing to be a linear function with gradient of one for
first-order methods, and two for second order methods.
In practice, the fast marching results come very close to these
criteria up to the limits of machine precision.
Figure 2 demonstrates the superiority of the
second-order fast marching formulation.
It is worth noting, at this point, that special treatment is required
at the source location, since the singularity in wavefront curvature
will cause numerical errors to propagate into the traveltime
solution. We surround the source with a constant
velocity box, within which we calculate traveltimes by ray-tracing.
Errors are inversely proportional to the radius of this
box. Therefore, if the radius of the box decrease with grid spacing,
errors will increase linearly,
reducing the accuracy of the method to first-order.
For full second-order accuracy, the box size should be independent of
grid spacing.
error
Figure 2 Average error against grid spacing for a
constant velocity model. The solid line corresponds to the
first-order eikonal solver, and the dashed line corresponds to the
second-order solver. The left panel has linear axes, whereas the
right panel is a 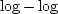 plot.
plot.




 marmousi
marmousi
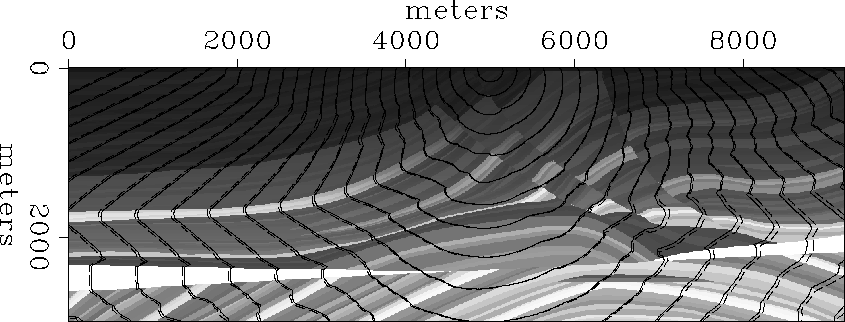
Figure 3 Traveltime contours calculated through the
Marmousi velocity model sampled at 4 m.
Solid line shows first-order results, and
dashed line shows second-order results.










Next: Computational cost
Up: Rickett & Fomel: Second-order
Previous: Fast marching and the
Stanford Exploration Project
4/20/1999

![]() plots of average error against
grid spacing to be a linear function with gradient of one for
first-order methods, and two for second order methods.
In practice, the fast marching results come very close to these
criteria up to the limits of machine precision.
Figure 2 demonstrates the superiority of the
second-order fast marching formulation.
plots of average error against
grid spacing to be a linear function with gradient of one for
first-order methods, and two for second order methods.
In practice, the fast marching results come very close to these
criteria up to the limits of machine precision.
Figure 2 demonstrates the superiority of the
second-order fast marching formulation.