By formulating our back projection operator in terms of vertical
travel-time (![]() ) rather than depth our reflector locations become
more stable Biondi et al. (1997); Clapp and Biondi (1998).
We show that the corresponding
back projection operator
is less sensitive to our initial velocity estimate. Therefore, our
back projection operator changes less from non-linear to non-linear
iteration, making the estimation less likely to get stuck in local minima.
) rather than depth our reflector locations become
more stable Biondi et al. (1997); Clapp and Biondi (1998).
We show that the corresponding
back projection operator
is less sensitive to our initial velocity estimate. Therefore, our
back projection operator changes less from non-linear to non-linear
iteration, making the estimation less likely to get stuck in local minima.
THEORY
Velocity estimation is fundamentally an inverse problem.
The correct solution is to do
full wave-form inversion Mora (1987); Tarantola (1986), but is generally impractical. Instead we start from
the idea that there is a non-linear operator that relates slowness (![]() )and travel time (
)and travel time (![]() ),
),
| (1) |
We then attempt to approximate ![]() by doing a two term Taylor
expansion around our initial guess at the slowness field (a version
of Newton's
minimization method):
by doing a two term Taylor
expansion around our initial guess at the slowness field (a version
of Newton's
minimization method):
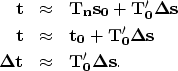 |
||
| (2) |
After inverting for ![]() , we have a new estimate for our slowness
field:
, we have a new estimate for our slowness
field:
| (3) |
|
newton
Figure 1 Newton's method applied to ray based tomography. | 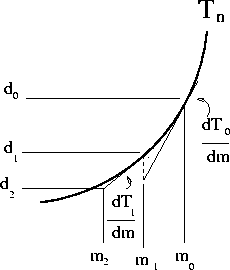 |
There are two problems with this approach. First, Newton's method is only guaranteed to converge to a local minima, we hope that by applying regularization Clapp and Biondi (1999) we can avoid this problem. And second, we are only using the first term in our Taylor expansion, which means that when our higher order derivatives are large, are descent direction will be wrong, and we will converge at a much slower rate. When using rays, this problem occurs when the initial guess at ray paths and reflector locations are too far from their correct locations.
We can obtain a measure of how inaccurate our linear approximation is
by looking at how much our linearized tomography operator changes
from non-linear iteration to non-linear iteration (the difference
erence between ![]() and
and ![]() .) The smaller the difference,
the more accurate our linearization, and
the less likely our estimate well diverge.
.) The smaller the difference,
the more accurate our linearization, and
the less likely our estimate well diverge.
By forming our tomography in (![]() ) rather than (z,x) space,
we reduce the change in
) rather than (z,x) space,
we reduce the change in ![]() from
from ![]() . The fundamental
reason is that our data is in time rather than depth.
In depth, reflector positions and layer boundaries
change significantly from
iteration to iteration, while in tau, they hardly
change at all Biondi et al. (1997).
. The fundamental
reason is that our data is in time rather than depth.
In depth, reflector positions and layer boundaries
change significantly from
iteration to iteration, while in tau, they hardly
change at all Biondi et al. (1997).