Nonlinear optimization arises from two causes:
iterate {

![$\bold W \quad\longleftarrow\quad{\bf diag}[w(\bold r)]$](img47.gif)
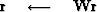
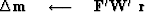

 }
}
where
Now let us see how the weighting functions relate
to robust estimation:
Notice in the code template that ![]() is applied twice
in the definition of
is applied twice
in the definition of ![]() .Thus
.Thus ![]() is the square root of the diagonal operator
in equation (13).
is the square root of the diagonal operator
in equation (13).
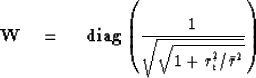 |
(14) |
Module weight_solver ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) implements the computational template above. In addition to the usual
set of arguments from the solver() subroutine
implements the computational template above. In addition to the usual
set of arguments from the solver() subroutine
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , it accepts a user-defined function (parameter
wght) for computing residual weights. Parameters
nmem and nfreq control the restarting schedule of
the iterative scheme.
, it accepts a user-defined function (parameter
wght) for computing residual weights. Parameters
nmem and nfreq control the restarting schedule of
the iterative scheme.
module weight_solver {
logical, parameter, private :: T = .true., F = .false.
contains
subroutine solver( oper, solv, x, dat, niter, nmem, nfreq, wght) {
interface {
integer function wght( res, w) {
real, dimension (:) :: res, w
}
integer function oper( adj, add, x, dat) {
logical, intent (in) :: adj, add
real, dimension (:) :: x, dat
}
integer function solv( forget, x, g, rr, gg) {
logical :: forget
real, dimension (:) :: x, g, rr, gg
}
}
real, dimension (:), intent (in) :: dat # data
real, dimension (:), intent (out) :: x # solution
integer, intent (in) :: niter, nmem, nfreq # iterations
real, dimension (size (x)) :: g # gradient
real, dimension (size (dat)) :: rr, gg, wt # res, CG, weight
integer :: i, stat
logical :: forget
rr = -dat; x = 0.; wt = 1.; forget = F # initialize
do i = 1, niter {
forget = (i > nmem) # restart
if( forget) stat = wght( rr, wt) # compute weighting
rr = rr * wt # rr = W (Fx - d)
stat = oper( T, F, g, wt*rr) # g = F' W' rr
stat = oper( F, F, g, gg) # gg = Fg
gg = gg * wt # gg = W F g
if( forget) forget = ( mod( i, nfreq) == 0) # periodic restart
stat = solv( forget, x, g, rr, gg) # step in x and rr
rr = - dat
stat = oper( F, T, x, rr) # rr = Fx - d
}
}
}
We can ask whether cgstep(), which was not designed
with nonlinear least-squares in mind, is doing the right thing
with the weighting function.
First, we know we are doing weighted linear least-squares correctly.
Then we recall that on the first iteration, the conjugate-directions
technique reduces to steepest descent,
which amounts to a calculation of
the scale factor ![]() with
with
| |
(15) |
Experience shows that difficulties arise when the weighting function varies rapidly from one iteration to the next. Naturally, the conjugate-direction method, which remembers the previous iteration, will have an inappropriate memory if the weighting function changes too rapidly. A practical approach is to be sure the changes in the weighting function are slowly variable.