![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) lead to
subroutine nicaf1(),
which allows for a different filter on each output data point.
lead to
subroutine nicaf1(),
which allows for a different filter on each output data point.
Filters sometimes change with time.
We sometimes observe signals whose spectrum changes with time.
Simple modifications to earlier convolution subroutines such as
icaf1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) lead to
subroutine nicaf1(),
which allows for a different filter on each output data point.
lead to
subroutine nicaf1(),
which allows for a different filter on each output data point.
module nicaf1 { # Nonstationary Internal Convolution, Adjoint is the Filter
real, dimension (:), pointer :: yy
integer :: n, na
#% _init (yy, n, na)
#% _lop (aa (n,na), rr (n))
integer a, r, y
do a = 1, na {
do r = na, n { y = r - a + 1
if( adj)
aa (r, a) += rr (r) * yy (y)
else
rr (r) += aa (r, a) * yy (y)
}}
}
Compared to those in icaf1(), these filter coefficients take much computer memory because there is a separate filter for every data point. Normally, the number of filter coefficients is many fewer than the number of data points, but here we have very many more. Indeed, there are na times more. Allowing time variation takes us from overdetermined to very undetermined. We can estimate all these filter coefficients by the usual deconvolution formulation (18)
| (55) |
| |
(56) |
Experience with missing data in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows that when the roughening operator
shows that when the roughening operator ![]() is a differential operator,
the number of iterations can be large.
We can speed the calculation immensely by ``preconditioning''.
When we define a new variable
is a differential operator,
the number of iterations can be large.
We can speed the calculation immensely by ``preconditioning''.
When we define a new variable ![]() by
by
![]() and insert it into (56) we get
and insert it into (56) we get
| |
(57) | |
| (58) |
Before viewing the full program,
we can reduce clutter in two ways.
First, because the smoothing and roughening operators
are somewhat arbitrary, we may as well replace
(58) by the simpler ![]() .The second way we can reduce clutter
is to simply drop the damping (58)
and keep only (57);
then to control the null space,
we need only to start
from a zero solution and limit the number of iterations.
As a practical matter,
without (58) we must find a good number of iterations and
with it we must find a good value for
.The second way we can reduce clutter
is to simply drop the damping (58)
and keep only (57);
then to control the null space,
we need only to start
from a zero solution and limit the number of iterations.
As a practical matter,
without (58) we must find a good number of iterations and
with it we must find a good value for ![]() .
.
The fitting (57) uses the operator ![]() .For
.For ![]() we can use subroutine nicaf1()
we can use subroutine nicaf1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
for the smoothing operator
,
for the smoothing operator ![]() we can use leaky integration
with subroutine leakint()
we can use leaky integration
with subroutine leakint() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
and for the constraints that a0=1 for all t,
we can throw in a code fragment to zero those
,
and for the constraints that a0=1 for all t,
we can throw in a code fragment to zero those ![]() and a few more for gapped filters.
The result is subroutine tvdecop().
and a few more for gapped filters.
The result is subroutine tvdecop().
module tvdec { # Linear operator for time-variable deconvolution
use leakint2
use nicaf1
real, dimension( ny*na), allocatable :: aa
#% _init( yy, ny, na, rho)
real, dimension( :), pointer :: yy
integer, intent( in) :: ny, na
real, intent( in) :: rho
call nicaf1_init( yy, ny, na)
call leakint2_init( ny, na, rho)
#% _lop( mod, dat)
integer stat1, stat2
if( adj) {
stat2 = nicaf1_lop ( adj, .false., aa, dat)
stat1 = leakint2_lop( adj, .true., mod, aa)
} else {
stat1 = leakint2_lop( adj, .false., mod, aa)
stat2 = nicaf1_lop ( adj, .true., aa, dat)
}
}
module leakint2 {
use leakint
integer :: n1, n2
#% _init (n1, n2, rho)
real, intent (in) :: rho
call leakint_init (rho)
#% _lop (x (n1,n2), y (n1,n2))
integer :: i2, stat1
do i2 = 1, n2
stat1 = leakint_lop (adj, .true., x (:,i2), y (:, i2))
}
Finally, we turn to the initialization.
Something new and slightly tricky arises here.
It is an example of a fitting goal with preconditioners.
If we were planning to start iterating from ![]() ,there would be no problem because
,there would be no problem because ![]() tells us that we would be starting from
tells us that we would be starting from ![]() .In fact, we must start from filters
.In fact, we must start from filters ![]() that
have a leading coefficient equal unity.
The correct starting
that
have a leading coefficient equal unity.
The correct starting ![]() must be the solution
to the equation
must be the solution
to the equation ![]() .Luckily, in this case, we can easily confirm that
the leaky integral of
.Luckily, in this case, we can easily confirm that
the leaky integral of
![]() is
is ![]() .Otherwise, the filter solver subroutine tvdcon()
is as uneventful as other simple solvers.
.Otherwise, the filter solver subroutine tvdcon()
is as uneventful as other simple solvers.
module tv_decon { # Time Variable (TV) Deconvolution
use tvdec
use cgstep_mod
use solver_mod
contains
subroutine tvdecon( rho, gap, na, yy, rr, niter) {
integer, intent( in) :: gap, na, niter
real, intent( in) :: rho
real, dimension( :), pointer :: yy
real, dimension( :), intent( out) :: rr
real, dimension( size( yy)*na) :: mm
logical, dimension( size( yy)*na) :: mask
real, dimension( size( rr)) :: dat
integer :: nt
nt = size( yy) ; dat = 0.
mm = 0. ; mm( 1) = 1. ; mm( 2:nt) = 1.- rho
mask = .false.; mask( :gap*nt) = .true.
call tvdec_init( yy, nt, na, rho)
call solver( tvdec_lop, cgstep, x0 = mm, x = mm, dat = dat,
known = mask, niter = niter, res = rr)
call cgstep_close()
call tvdec_close()
}
}
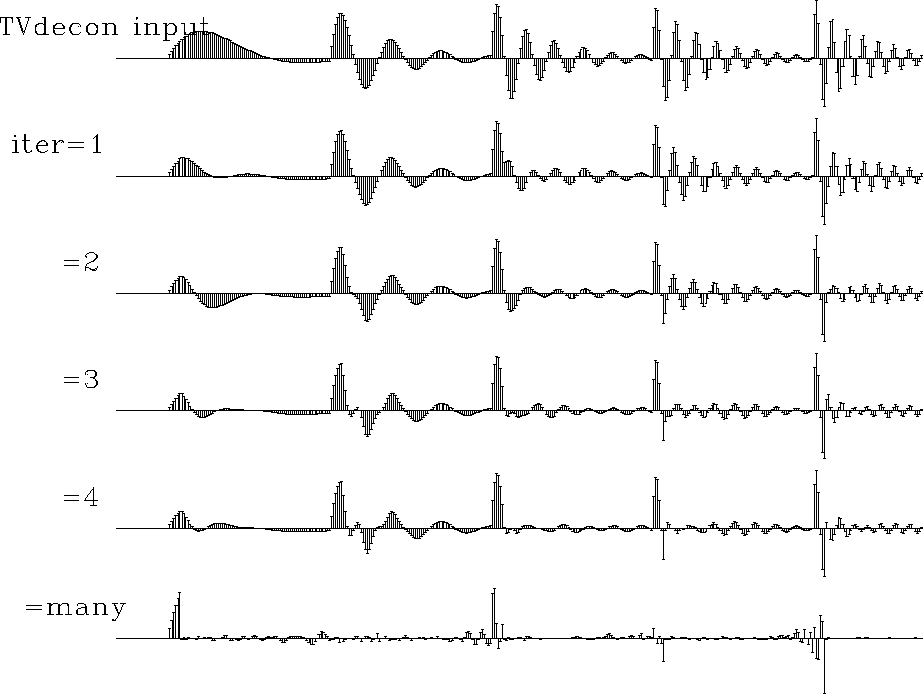
Figure 16 shows a synthetic data example using these programs. As we hope for deconvolution, events are compressed. The compression is fairly good, even though each event has a different spectrum. What is especially pleasing is that satisfactory results are obtained in truly small numbers of iterations (about three). The example is for two free filter coefficients and a gap of 6. Observe that the first 6 points of waveforms are preserved in the early iterations only.
 |
I hope also to find a test case with field data, but experience in seismology is that spectral changes are slow, which implies unexciting results. Many interesting examples should exist in two- and three-dimensional filtering, however, because reflector dip is always changing and that changes the spatial spectrum.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . HINTS:
Do not try to write all the matrix elements.
Instead draw short lines to indicate rows or columns.
As a ``warm up'' consider a simpler case where one filter
is used on the first half of the data and another filter
for the other half.
Then upgrade that solution from two to about ten filters.
. HINTS:
Do not try to write all the matrix elements.
Instead draw short lines to indicate rows or columns.
As a ``warm up'' consider a simpler case where one filter
is used on the first half of the data and another filter
for the other half.
Then upgrade that solution from two to about ten filters.