




Next: About this document ...
Up: Empty bins and inverse
Previous: SEARCHING THE SEA OF
In Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we defined linear interpolation
we defined linear interpolation
as the extraction of values from between mesh points.
In a typical setup (occasionally the role of data and model are swapped),
a model is given on a uniform mesh
and we solve the easy problem of extracting values
between the mesh points with subroutine lint1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The genuine problem is the inverse problem, which we attack here.
Data values are sprinkled all around,
and we wish to find a function on a uniform mesh
from which we can extract that data by linear interpolation.
The adjoint operator for subroutine lint1()
simply piles data back into its proper location in model space
without regard to how many data values land in each region.
Thus some model values may have many data points added
to them while other model values get none.
We could interpolate by minimizing the energy in the gradient,
or that in the second derivative of the model,
or that in the output of any other roughening filter
applied to the model.
.
The genuine problem is the inverse problem, which we attack here.
Data values are sprinkled all around,
and we wish to find a function on a uniform mesh
from which we can extract that data by linear interpolation.
The adjoint operator for subroutine lint1()
simply piles data back into its proper location in model space
without regard to how many data values land in each region.
Thus some model values may have many data points added
to them while other model values get none.
We could interpolate by minimizing the energy in the gradient,
or that in the second derivative of the model,
or that in the output of any other roughening filter
applied to the model.
Formalizing now our wish
that data 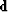 be extractable by linear interpolation
be extractable by linear interpolation 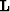 ,from a model
,from a model 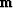 ,and our wish that application of a roughening filter
with an operator
,and our wish that application of a roughening filter
with an operator 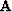 have minimum energy, we write the fitting goals:
have minimum energy, we write the fitting goals:
| 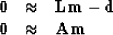 |
(20) |
Suppose we take the roughening filter to be the second difference operator
(1,-2,1)
scaled by a constant  ,and suppose we have a data point near each end of the model
and a third data point exactly in the middle.
Then,
for a model space 7 points long,
the fitting goal could look like
,and suppose we have a data point near each end of the model
and a third data point exactly in the middle.
Then,
for a model space 7 points long,
the fitting goal could look like
| ![\begin{displaymath}
{
\left[
\begin{array}
{rrrrrr}
.8 & .2 & . & . & . & . \...
...
\bold r_m
\end{array} \right]
\quad \approx \ \bold 0
} \end{displaymath}](img68.gif) |
(21) |
The residual vector has two parts,
a data part 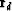 on top
and a model part
on top
and a model part 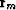 on the bottom.
The data residual
should vanish except where contradictory data values
happen to lie in the same place.
The model residual is the roughened model.
on the bottom.
The data residual
should vanish except where contradictory data values
happen to lie in the same place.
The model residual is the roughened model.
Two fitting goals (20) are so common in practice
that it is convenient to adopt our least-square fitting
subroutine solver ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) accordingly.
The modification
is shown in module reg_solver
accordingly.
The modification
is shown in module reg_solver ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
In addition to specifying the ``data fitting'' operator
.
In addition to specifying the ``data fitting'' operator 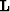 (parameter oper),
we need to pass the ``model regularization'' operator
(parameter oper),
we need to pass the ``model regularization'' operator 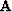 (parameter reg) and the
size of its output (parameter nreg) for proper memory allocation.
(When I first looked at module reg_solver I was appalled
by the many lines of code, especially all the declarations.
Then I realized how much much worse was Fortran 77 where
I needed to write a new solver for every pair of operators.
This one solver module works for all operator pairs
and for many optimization descent strategies
because these ``objects'' are arguments.
These objects require declarations that are more complicated
than the simple objects of Fortran 77.)
(parameter reg) and the
size of its output (parameter nreg) for proper memory allocation.
(When I first looked at module reg_solver I was appalled
by the many lines of code, especially all the declarations.
Then I realized how much much worse was Fortran 77 where
I needed to write a new solver for every pair of operators.
This one solver module works for all operator pairs
and for many optimization descent strategies
because these ``objects'' are arguments.
These objects require declarations that are more complicated
than the simple objects of Fortran 77.)
module reg_solver {
logical, parameter, private :: T = .true., F = .false.
contains
subroutine solver_reg( oper, solv, reg, nreg, x, dat, niter, eps, x0) {
optional :: x0
interface {
integer function oper( adj, add, x, dat) {
logical, intent( in) :: adj, add
real, dimension( :) :: x, dat
}
integer function reg( adj, add, x, dat) {
logical, intent( in) :: adj, add
real, dimension( :) :: x, dat
}
integer function solv( forget, x, g, rr, gg) {
logical :: forget
real, dimension( :) :: x, g, rr, gg
}
}
real, dimension( :), intent( in) :: dat, x0 # data, initial
real, dimension( :), intent( out) :: x # solution
real, intent( in) :: eps # scaling
integer, intent( in) :: niter, nreg # iterations, size
real, dimension( size( x)) :: g # gradient
real, dimension( size( dat) + nreg), target :: rr, gg # residual, conj grad
real, dimension( :), pointer :: rd,rm,gd,gm
integer :: i, stat1, stat2, stat
rm => rr( 1: nreg); rd => rr( 1 + nreg:) # model and data resids
gm => gg( 1: nreg); gd => gg( 1 + nreg:) # model and data grads
rd = - dat # initialize r_d
if( present( x0)) {
stat1 = oper( F, T, x0, rd) # r_d = L x0 - dat
stat2 = reg( F, F, x0, rm) # r_m = eps A x0
rm = rm*eps #
x = x0 } # start with x0
else { x = 0.; rm = 0.} # start with zero
do i = 1, niter {
stat1 = oper( T, F, g, rd) # g = L' r_d
gm = rm*eps #
stat2 = reg( T, T, g, gm) # g = L' r_d + eps A' r_m
stat1 = oper( F, F, g, gd) # g_d = L g
stat2 = reg( F, F, g, gm) # g_m = eps A g
gm = gm*eps #
stat = solv( F, x, g, rr, gg) # step in x and rr
}
}
}
First we load the data part of the residual
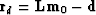 and
the model part of the residual
and
the model part of the residual
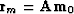 .After the initialization, the subroutine
invint1() begins an iteration loop by first computing
the proposed model perturbation
.After the initialization, the subroutine
invint1() begins an iteration loop by first computing
the proposed model perturbation 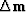 with the adjoint operator:
with the adjoint operator:
| ![\begin{displaymath}
\Delta \bold m
\quad\longleftarrow\quad
\left[
\begin{arr...
...\begin{array}
{c}
\bold r_d \\ \bold r_m
\end{array} \right]\end{displaymath}](img73.gif) |
(22) |
Using this value of 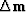 ,we can
find the implied change in residual
,we can
find the implied change in residual 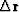 as
as
| ![\begin{displaymath}
\Delta
\left[
\begin{array}
{c}
\bold r_d \\ \bold r_m
...
...c}
\bold L \\ \bold A
\end{array} \right]
\
\Delta \bold m\end{displaymath}](img74.gif) |
(23) |
and the last thing in the loop is to use
the optimization step function solv()
to choose the length of the step size
and to choose how much of the previous step to include.
An example of using the new solver is subroutine invint1
I chose to implement the model roughening operator 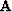 with the convolution subroutine tcai1()
with the convolution subroutine tcai1() ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
which has transient end effects
(and an output length equal to the input length plus the filter length).
The adjoint of subroutine tcai1() suggests perturbations
in the convolution input (not the filter).
,
which has transient end effects
(and an output length equal to the input length plus the filter length).
The adjoint of subroutine tcai1() suggests perturbations
in the convolution input (not the filter).
module invint { # invint - INVerse INTerpolation in 1-D.
use lint1
use tcai1
use cgstep_mod
use reg_solver
contains
subroutine invint1( niter, coord, dd, o1, d1, aa, mm, eps) {
integer, intent (in) :: niter # iterations
real, intent (in) :: o1, d1, eps # axis, scale
real, dimension (:), pointer :: coord, aa # aa is filter
real, dimension (:), intent (in) :: dd # data
real, dimension (:), intent (out) :: mm # model
integer :: nreg # size of A m
nreg = size( aa) + size( mm) # transient
call lint1_init( o1, d1, coord ) # interpolation
call tcai1_init( aa, size( mm)) # filtering
call solver_reg( lint1_lop, cgstep, tcai1_lop, nreg, mm, dd, niter, eps)
call cgstep_close( )
}
}
Figure 11 shows an example for a (1,-2,1) filter with 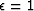 .The continuous curve representing the model
.The continuous curve representing the model 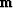 passes through the data points.
Because the models are computed with transient convolution end-effects,
the models tend to damp linearly to zero outside the region where
signal samples are given.
passes through the data points.
Because the models are computed with transient convolution end-effects,
the models tend to damp linearly to zero outside the region where
signal samples are given.
im1-2+190
Figure 11
Sample points and estimation of a continuous function through them.
|
| 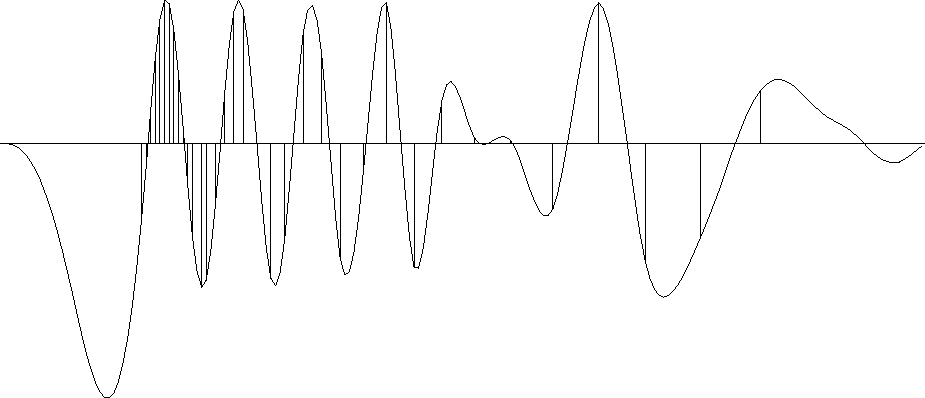 |





To show an example where the result is clearly a theoretical answer,
I prepared another figure with the simpler filter (1,-1).
When we minimize energy in the first derivative of the waveform,
the residual distributes itself uniformly
between data points
so the solution there is a straight line.
Theoretically it should be a straight line
because a straight line has a vanishing second derivative,
and that condition arises by differentiating by 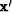 ,the minimized quadratic form
,the minimized quadratic form
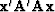 , and getting
, and getting
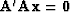 .(By this logic, the curves between data points in Figure 11
must be cubics.)
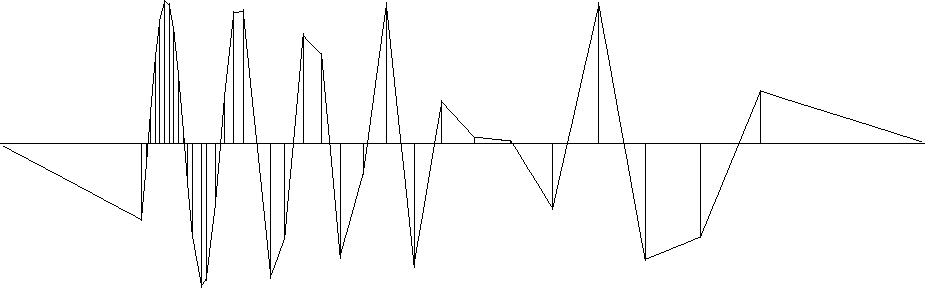
The (1,-1) result is shown in Figure 12.
.(By this logic, the curves between data points in Figure 11
must be cubics.)
The (1,-1) result is shown in Figure 12.
im1-1a90
Figure 12
The same data samples
and a function through them that minimizes
the energy in the first derivative.
|
|  |










Next: About this document ...
Up: Empty bins and inverse
Previous: SEARCHING THE SEA OF
Stanford Exploration Project
2/27/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The genuine problem is the inverse problem, which we attack here.
Data values are sprinkled all around,
and we wish to find a function on a uniform mesh
from which we can extract that data by linear interpolation.
The adjoint operator for subroutine lint1()
simply piles data back into its proper location in model space
without regard to how many data values land in each region.
Thus some model values may have many data points added
to them while other model values get none.
We could interpolate by minimizing the energy in the gradient,
or that in the second derivative of the model,
or that in the output of any other roughening filter
applied to the model.
.
The genuine problem is the inverse problem, which we attack here.
Data values are sprinkled all around,
and we wish to find a function on a uniform mesh
from which we can extract that data by linear interpolation.
The adjoint operator for subroutine lint1()
simply piles data back into its proper location in model space
without regard to how many data values land in each region.
Thus some model values may have many data points added
to them while other model values get none.
We could interpolate by minimizing the energy in the gradient,
or that in the second derivative of the model,
or that in the output of any other roughening filter
applied to the model.
![\begin{displaymath}
{
\left[
\begin{array}
{rrrrrr}
.8 & .2 & . & . & . & . \...
...
\bold r_m
\end{array} \right]
\quad \approx \ \bold 0
} \end{displaymath}](img68.gif)

