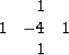Next: Causality in two-dimensions
Up: FILTERING ON A HELIX
Previous: Examples of simple 2-D
Let us unroll the filter helix seen in Figure 2
and see what we have.
Start from the idea that a 2-D filter is generally made
from a cluster of values near one another in two dimensions
similar to the Laplacian operator in the figure.
We see that in the helical approach,
a 2-D filter is a 1-D filter containing some long intervals of zeros.
The intervals are about the length of a 1-D seismogram.
Our program for 2-D convolution with a 1-D convolution program,
could convolve with the somewhat long 1-D strip,
but it is much more cost effective to ignore the many zeros,
which is what we do.
We do not multiply by the backside zeros, nor do we even store them in memory.
Whereas an ordinary convolution program would do time shifting
by a code line like iy=ix+lag,
Module
helicon ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ignores the many zero filter values on backside of the tube
by using the code iy=ix+lag(ia)
where a counter ia ranges over the nonzero filter coefficients.
Before operator helicon is invoked,
we need to prepare two lists,
one list containing nonzero filter coefficients aa(ia),
and the other list containing the corresponding lags lag(ia)
measured to include multiple wraps around the helix.
For example, the 2-D Laplace operator
ignores the many zero filter values on backside of the tube
by using the code iy=ix+lag(ia)
where a counter ia ranges over the nonzero filter coefficients.
Before operator helicon is invoked,
we need to prepare two lists,
one list containing nonzero filter coefficients aa(ia),
and the other list containing the corresponding lags lag(ia)
measured to include multiple wraps around the helix.
For example, the 2-D Laplace operator
| 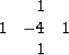 |
(4) |
can be thought of as the 1-D filter
| 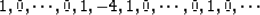 |
(5) |
The first filter coefficient in equation (5)
is +1 as implicit to module helicon.
To apply the Laplacian on a  mesh
requires the filter inputs:
mesh
requires the filter inputs:
i lag(i) aa(i)
--- ------ -----
1 999 1
2 1000 -4
3 1001 1
4 2000 1
Operator helicon did the convolution job for Figure 1.
The first half of operator helicon does adjoint filtering.
The adjoint of filtering is filtering backwards.
The ends of the 1-D axis are a little trickier than you might imagine,
but there is no need to examine them now.
(One end is transient, the other truncated.)
module helicon { # Convolution, inverse to deconvolution.
# Designed for gapped filters (helical 2-D, 3-D, etc).
# Requires the filter be causal with an implicit "1." at the onset.
real, dimension (:), pointer :: aa
integer, dimension (:), pointer :: lag
#% _init ( aa, lag)
if( any( lag <= 0)) call erexit ("Filter is not causal")
#% _lop ( xx, yy)
integer iy, ix, ia
if( adj) # zero lag
xx += yy
else
yy += xx
do ia= 1, size(aa) {
do ix= 1, size(xx)-lag(ia) { iy = ix + lag(ia)
if( adj)
xx(ix) += yy(iy) * aa(ia)
else
yy(iy) += xx(ix) * aa(ia)
}}
}
The module polydiv ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) was coded in such a way that it works on a helix.
was coded in such a way that it works on a helix.





Next: Causality in two-dimensions
Up: FILTERING ON A HELIX
Previous: Examples of simple 2-D
Stanford Exploration Project
2/27/1998
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ignores the many zero filter values on backside of the tube
by using the code iy=ix+lag(ia)
where a counter ia ranges over the nonzero filter coefficients.
Before operator helicon is invoked,
we need to prepare two lists,
one list containing nonzero filter coefficients aa(ia),
and the other list containing the corresponding lags lag(ia)
measured to include multiple wraps around the helix.
For example, the 2-D Laplace operator
ignores the many zero filter values on backside of the tube
by using the code iy=ix+lag(ia)
where a counter ia ranges over the nonzero filter coefficients.
Before operator helicon is invoked,
we need to prepare two lists,
one list containing nonzero filter coefficients aa(ia),
and the other list containing the corresponding lags lag(ia)
measured to include multiple wraps around the helix.
For example, the 2-D Laplace operator