|
|
|
|
Estimation of Q from surface-seismic reflection data in data space and image space |
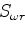 is the slowness at the reference frequency
is the slowness at the reference frequency 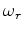 .
.
Having the new velocity/slowness, I obtain the new single square root as
| (12) |
This new SSR can be approximated into a simplified form by using Taylor expansion around reference slowness 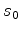 and reference quality factor
and reference quality factor 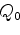 :
:
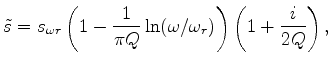 |
(14) |
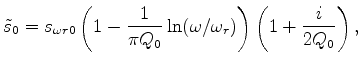 |
(15) |
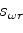 is the reference slowness at the reference frequency. The first two terms of equation 13 describe the split-step migration. The third term is the high-order correction, which allows for pseudo-screen migration.
is the reference slowness at the reference frequency. The first two terms of equation 13 describe the split-step migration. The third term is the high-order correction, which allows for pseudo-screen migration.
The single square root for FFD migration is shown as follows:
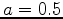 and
and 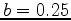 for 45-degree migration.
for 45-degree migration.
In addition, I can rewrite Q migration in a matrix form to conveniently compare with the conventional migration. The conventional migration can be written in the following matrix form:
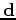 is the data,
is the data, 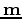 is the model,
is the model, 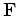 is the migration operator, and the superscript
is the migration operator, and the superscript 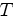 indicates the matrix transpose.
indicates the matrix transpose.
The downward continuation migration with Q can be written as
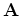 is the attenuation operator, which consists of real numbers less than
is the attenuation operator, which consists of real numbers less than 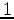 .
.
Equation 18 indicates that the migrated model will be further attenuated, with the attenuation operator 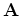 being applied to the attenuated modeled data. Therefore, Q migration will compensate for the phase change, but will not compensate for the amplitude loss due to attenuation.
being applied to the attenuated modeled data. Therefore, Q migration will compensate for the phase change, but will not compensate for the amplitude loss due to attenuation.
In this section, I apply Q migration to the modeled data in Figures 1(a) and 1(b). Figure 3(a) shows the conventional migration of the non-attenuated data in Figure 1(b), which images the reflector at 1500 m depth. Figures 3(b) and 3(c) show the conventional migration and Q migration of the attenuated data in Figure 1(a). The wavelets in Figure 3(c) are stretched in comparison to the ones in Figure 3(a). This result confirms that Q migration further attenuates the data, instead of compensating for its amplitude loss.
|
|
|
|
Estimation of Q from surface-seismic reflection data in data space and image space |