|
|
|
|
Estimation of Q from surface-seismic reflection data in data space and image space |
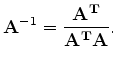 |
(20) |
One thing to notice is that the compensated amplitude in equation 19 contains both attenuation and an evanescent wave. However, only the attenuation part needs to be compensated. Therefore I need to remove the evanescent wave from the amplitude compensation. For a single frequency, the attenuation operator is shown as follows:
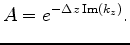 |
(21) |
After removing the evanescent part from the amplitude compensation, the inverse attenuation operator is shown as follows:
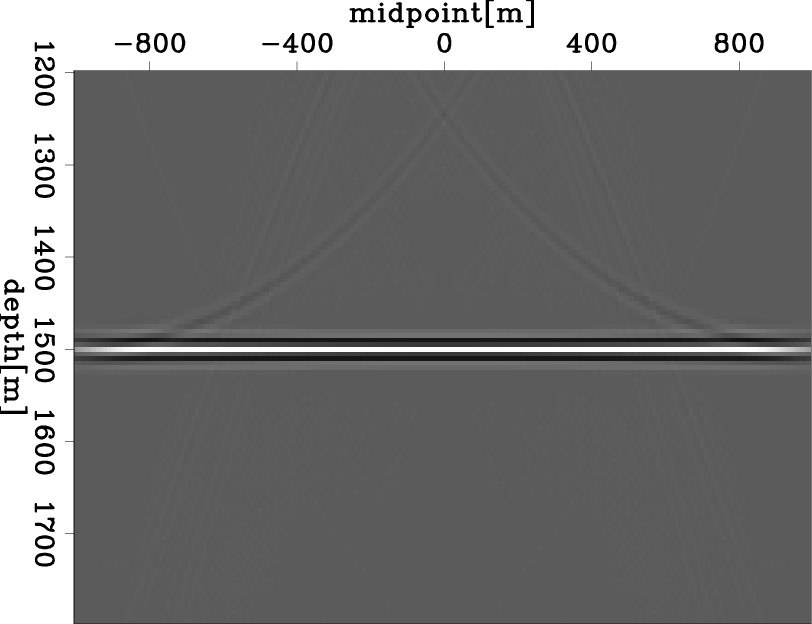
Figure 3(d) shows Q compensation on the attenuated data, showing exactly the same result as Figure 3(a), which has no attenuation in either forward propagation or backward imaging. This result indicates that Q compensation adequately restores the amplitude loss caused by attenuation.



|
|---|
|
ctrl,nqmig,qncp,qmig
Figure 3. Given the 2D synthetic example, (a) conventional migration on non-attenuated data; (b) conventional migration on attenuated data; (c) Q migration on attenuated data; (d) Q compensation on attenuated data. |
|
|
|
|
|
|
Estimation of Q from surface-seismic reflection data in data space and image space |