|
|
|
|
Enhanced interpreter-aided salt-boundary extraction using shape deformation |
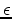 -insensitive L1 norm:
-insensitive L1 norm:
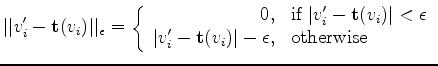 |
(2) |
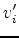 are sought along the contour’s normal direction
are sought along the contour’s normal direction
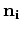 , we constrain the desired mapping
, we constrain the desired mapping
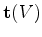 to displace
to displace 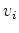 along direction
along direction
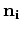 as well:
as well:
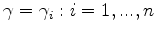 . Since points in
. Since points in 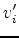 are found along the normal directions of the original contour
are found along the normal directions of the original contour 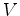 as well, we have
as well, we have
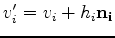 . Then the previous problem 1 becomes
. Then the previous problem 1 becomes
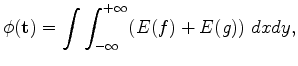
where
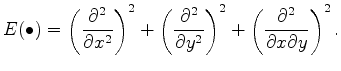
The nice thing about this choice of bending-energy is that we know in advance, given all mappings that satisfy constraint 3, the mapping specified by thin-plate spline interpolation will minimize the bending-energy (Bookstein, 1989). In other words, the solution
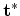 to the optimization problem 4 must be the thin-plate spline interpolation that maps
to the optimization problem 4 must be the thin-plate spline interpolation that maps
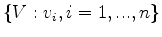 to
to
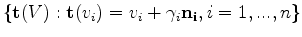 .
Given that
.
Given that
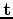 must be a thin-plate spline interpolation, we can express
must be a thin-plate spline interpolation, we can express
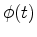 with the vector
with the vector 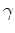 . Therefore, this variational problem (where the optimization parameters are functions not numbers) turns into a much simpler numerical convex optimization problem. We just need to find the optimal
. Therefore, this variational problem (where the optimization parameters are functions not numbers) turns into a much simpler numerical convex optimization problem. We just need to find the optimal 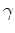 for the problem below:
for the problem below:
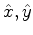 is the vector representation of the
is the vector representation of the 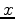 and
and 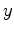 coordinates of the points in set
coordinates of the points in set
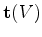 , and
, and 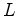 is a semi-positive definite matrix defined by known quantities.
is a semi-positive definite matrix defined by known quantities.
Using the standard SVM technique, we can instead solve the dual problem of 5 according to the K.K.T.(Karush-Kuhn-Tucker) conditions. It ends up being a standard quadratic programming problem with both upper and lower bounds.
|
|
|
|
Enhanced interpreter-aided salt-boundary extraction using shape deformation |