|
|
|
|
Enhanced interpreter-aided salt-boundary extraction using shape deformation |
We represent the known contour on the template image as a set of landmark points,
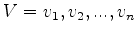 where
where
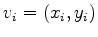 (in 2-D Cartesian coordinates). Wang et al. (2001) describe the skeleton of this algorithm as follows:
(in 2-D Cartesian coordinates). Wang et al. (2001) describe the skeleton of this algorithm as follows:
``For each landmark, the proposed method first identifies a set of possible corresponding landmark points
on the input image, where
. Then conceptually the deformation is solved in two major steps:
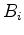 from the landmark set
from the landmark set  such that
such that
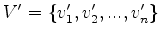 is located in or near the true object boundary in the input image.
is located in or near the true object boundary in the input image.
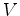 to match
to match 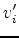 while keeping the general shape characteristics of
while keeping the general shape characteristics of 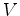 . ''
. ''
|
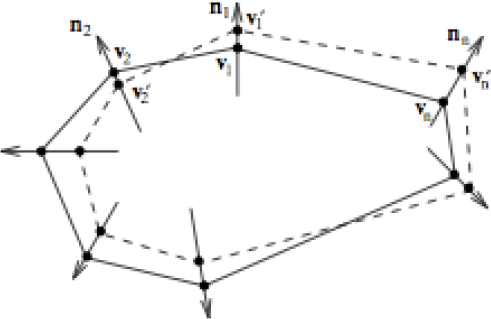
Fig2-deform
Figure 2. Landmark-based shape deformation, from Wang et al. (2001). |
|
|---|---|
|
|
For the first step, we search the candidate points in set 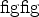 along a short line segment that centers around point
along a short line segment that centers around point 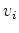 and aligns to the contour’s normal direction
and aligns to the contour’s normal direction
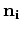 .
It is difficult to determine the best landmark point
.
It is difficult to determine the best landmark point 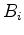 from all candidates in
from all candidates in 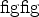 at the first try. Therefore, we just choose randomly an element in each
at the first try. Therefore, we just choose randomly an element in each 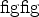 to form the initial set
to form the initial set 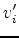 and iterate this selection process a few times. During each iteration, we update the set
and iterate this selection process a few times. During each iteration, we update the set 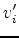 such that
such that 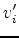 more likely contains the correct corresponding landmarks.
more likely contains the correct corresponding landmarks.
The next deformation step is formulated by finding the optimal solution to an objective function which takes into account both the goal of deforming the points in 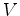 into the current landmark set
into the current landmark set 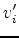 and the goal of preserving the prior shape
and the goal of preserving the prior shape 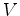 (using the bending-energy formula from (Bookstein, 1989)). The optimization goal is
(using the bending-energy formula from (Bookstein, 1989)). The optimization goal is
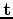 defines the deformation from
defines the deformation from 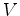 to
to 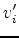 as a mapping; i.e.
as a mapping; i.e.
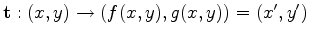 . Function
. Function 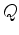 describes the term that penalizes the mismatch between
describes the term that penalizes the mismatch between 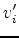 (the landmarks we found on the input image) and the mapping defined by
(the landmarks we found on the input image) and the mapping defined by
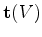 .
The
.
The 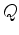 term corresponds to the first goal, deforming the landmarks in set
term corresponds to the first goal, deforming the landmarks in set 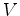 to those in
to those in 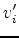 . Function
. Function
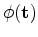 is a regularization term that tries to force the mapping
is a regularization term that tries to force the mapping
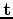 to be smooth, in other words, preserving the global shape information of the original
to be smooth, in other words, preserving the global shape information of the original 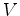 .
We add a
.
We add a 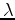 parameter to balance the weights of the two terms, Q and
parameter to balance the weights of the two terms, Q and  . The choice of
. The choice of 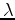 is up to the user's judgment. After mathematical simplification, this optimization can be solved easily using the classical SVM(Support Vector Machine) regression technique (as a quadratic programming problem of size
is up to the user's judgment. After mathematical simplification, this optimization can be solved easily using the classical SVM(Support Vector Machine) regression technique (as a quadratic programming problem of size 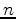 ). Moreover, the badly fitted components in set
). Moreover, the badly fitted components in set 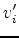 are identified as the support-vectors. We update the set
are identified as the support-vectors. We update the set 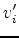 by replacing those support-vectors with other candidates in
by replacing those support-vectors with other candidates in 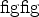 , such that the new set
, such that the new set 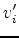 would achieve better fitting.
would achieve better fitting.
|
|
|
|
Enhanced interpreter-aided salt-boundary extraction using shape deformation |