 |
 |
 |
 | Residual moveout-based wave-equation migration velocity analysis in 3-D |  |
![[pdf]](icons/pdf.png) |
Next: Gaussian anomaly example
Up: 3-D RMO WEMVA method
Previous: 2-D Theory Review
As we shift from 2-D seismic surveys to 3-D ones, two extra dimensions (cross-line axis 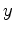 and subsurface azimuth
and subsurface azimuth 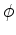 ) are added to our seismic image. Therefore we denote the prestack image as
) are added to our seismic image. Therefore we denote the prestack image as
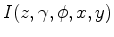 . Assuming there are
. Assuming there are 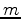 values for
values for 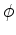 , then
, then
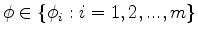 .
Now the maximum-stack-power objective function 1 can be generalized to
.
Now the maximum-stack-power objective function 1 can be generalized to
![$\displaystyle J(s) = \frac{1}{2} \sum_{x,y}\sum_{z} {\left[\sum_{\phi_i} \sum_{\gamma} \; I(z,\gamma,\phi_i,x,y;s) \right]}^2,$](img64.png) |
(11) |
in which we stack the gather along both 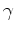 and
and 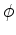 axes.
axes.
The next step is to choose a proper residual moveout parameterization for the 3-D ADCIGs, in which the moveout is a surface (defined by
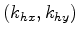 ) rather than a curve (of
) rather than a curve (of 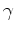 ). There are certainly more than one way to design such parameterization.
As an initial attempt, we choose a straightforward approach, in which we separate the moveout surface into individual curves by azimuth
). There are certainly more than one way to design such parameterization.
As an initial attempt, we choose a straightforward approach, in which we separate the moveout surface into individual curves by azimuth 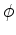 . For each azimuth angle
. For each azimuth angle 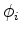 , we assign the curvature parameter
, we assign the curvature parameter 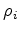 and the static shift parameter
and the static shift parameter 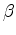 , respectively.
Notice that all the curves share the same
, respectively.
Notice that all the curves share the same 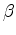 parameter, because the center of the move-out surface at (
parameter, because the center of the move-out surface at (
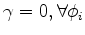 ) is shared by all curves.
) is shared by all curves.
Under this parameterization, the 3-D counterpart of objective function 3 would be
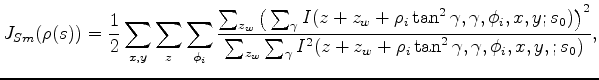 |
(12) |
where
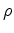 becomes a vector,
becomes a vector,
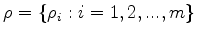 . The gradient formula 4 now turns into
. The gradient formula 4 now turns into
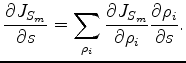 |
(13) |
Because each 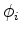 is treated separately, we can compute
is treated separately, we can compute
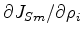 in exactly the same way as we do in the 2-D case.
in exactly the same way as we do in the 2-D case.
Analogously, we can define an auxiliary objective function for each image point that uncovers the
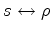 relationship:
relationship:
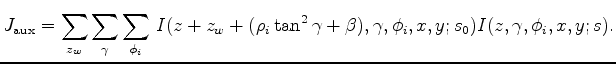 |
(14) |
Using the same trick of finding partial derivatives for implicit functions, equation 6 is generalized as
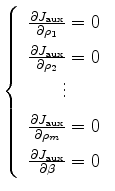 |
(15) |
We differentiate equation 15 with respect to 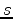 :
:
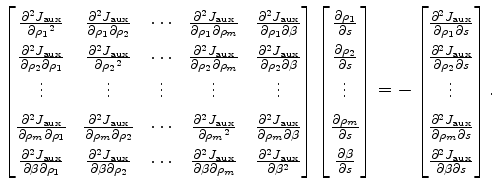 |
(16) |
We can calculate the 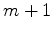 by
by 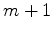 Jacobian matrix elements and the right-hand side based on equation 14:
Jacobian matrix elements and the right-hand side based on equation 14:
Denoting matrix
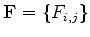 to be the inverse of the Jacobian, then
to be the inverse of the Jacobian, then
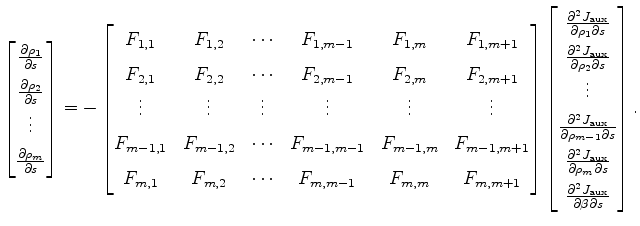 |
(18) |
Finally, plugging equation 18 and 17 back into the model gradient expression 13, we get
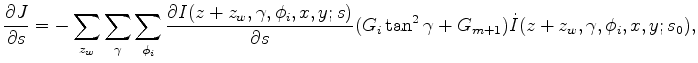 |
(19) |
in which
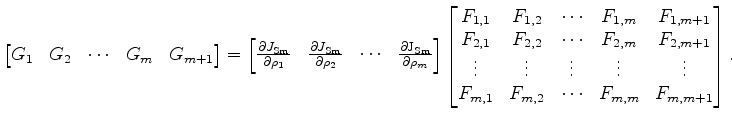 |
(20) |
In practice, there are some caveats when taking the inverse of the Jacobian matrix. The Jacobian can be ill-conditioned when all elements in one row or column are close to zero.
For example, if the image point is not illuminated from a certain azimuth direction 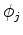 , i.e.
, i.e.
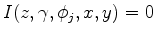 , then the
, then the 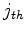 row and column of the Jacobian would be zero.
In order to avoid numerical overflow under this circumstance, we pre-exclude those azimuth angles with poor illumination energy from the Jacobian, and we invert a subset of the original Jacobian that contains only image gathers at well-illuminated azimuth angles.
row and column of the Jacobian would be zero.
In order to avoid numerical overflow under this circumstance, we pre-exclude those azimuth angles with poor illumination energy from the Jacobian, and we invert a subset of the original Jacobian that contains only image gathers at well-illuminated azimuth angles.
 |
 |
 |
 | Residual moveout-based wave-equation migration velocity analysis in 3-D |  |
![[pdf]](icons/pdf.png) |
Next: Gaussian anomaly example
Up: 3-D RMO WEMVA method
Previous: 2-D Theory Review
2012-05-10
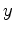 and subsurface azimuth
and subsurface azimuth 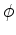 ) are added to our seismic image. Therefore we denote the prestack image as
) are added to our seismic image. Therefore we denote the prestack image as
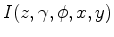 . Assuming there are
. Assuming there are 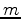 values for
values for 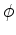 , then
, then
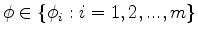 .
Now the maximum-stack-power objective function 1 can be generalized to
.
Now the maximum-stack-power objective function 1 can be generalized to
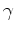 and
and 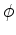 axes.
axes.
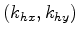 ) rather than a curve (of
) rather than a curve (of 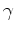 ). There are certainly more than one way to design such parameterization.
As an initial attempt, we choose a straightforward approach, in which we separate the moveout surface into individual curves by azimuth
). There are certainly more than one way to design such parameterization.
As an initial attempt, we choose a straightforward approach, in which we separate the moveout surface into individual curves by azimuth 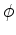 . For each azimuth angle
. For each azimuth angle 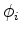 , we assign the curvature parameter
, we assign the curvature parameter 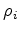 and the static shift parameter
and the static shift parameter 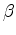 , respectively.
Notice that all the curves share the same
, respectively.
Notice that all the curves share the same 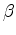 parameter, because the center of the move-out surface at (
parameter, because the center of the move-out surface at (
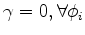 ) is shared by all curves.
) is shared by all curves.
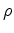 becomes a vector,
becomes a vector,
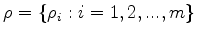 . The gradient formula 4 now turns into
. The gradient formula 4 now turns into
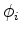 is treated separately, we can compute
is treated separately, we can compute
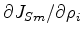 in exactly the same way as we do in the 2-D case.
in exactly the same way as we do in the 2-D case.
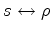 relationship:
relationship:
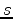 :
:

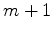 by
by 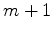 Jacobian matrix elements and the right-hand side based on equation 14:
Jacobian matrix elements and the right-hand side based on equation 14:
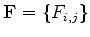 to be the inverse of the Jacobian, then
to be the inverse of the Jacobian, then
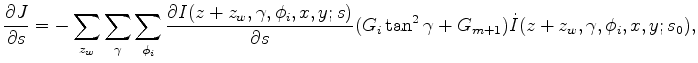
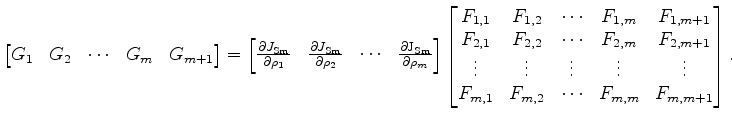
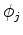 , i.e.
, i.e.
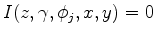 , then the
, then the 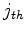 row and column of the Jacobian would be zero.
In order to avoid numerical overflow under this circumstance, we pre-exclude those azimuth angles with poor illumination energy from the Jacobian, and we invert a subset of the original Jacobian that contains only image gathers at well-illuminated azimuth angles.
row and column of the Jacobian would be zero.
In order to avoid numerical overflow under this circumstance, we pre-exclude those azimuth angles with poor illumination energy from the Jacobian, and we invert a subset of the original Jacobian that contains only image gathers at well-illuminated azimuth angles.