|
|
|
|
Residual moveout-based wave-equation migration velocity analysis in 3-D |
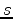 is the model slowness, and
is the model slowness, and
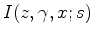 is the prestack image (ADCIGs) migrated with
is the prestack image (ADCIGs) migrated with 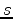 .
.
Objective functions defined this way are prone to cycle-skipping (Symes, 2008). To tackle this issue, we approximate objective function 1 with the following one:
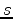 is the model slowness,
is the model slowness,
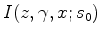 is the prestack image migrated with some initial slowness
is the prestack image migrated with some initial slowness 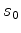 , and
, and
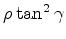 is the residual moveout (RMO) function we choose to characterize the kinematic difference (Biondi and Symes, 2004) between
is the residual moveout (RMO) function we choose to characterize the kinematic difference (Biondi and Symes, 2004) between
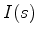 and
and 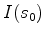 .
.
The meaning of equation 2 can be easily explained. As the model changes from 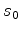 to
to 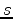 , it leads to the change of the image kinematics between
, it leads to the change of the image kinematics between
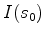 and
and 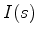 , where the differences are characterized by the moveout parameter
, where the differences are characterized by the moveout parameter 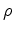 .
Since
.
Since 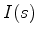 will be kinematically the same as
will be kinematically the same as 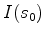 being applied moveout
being applied moveout 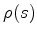 , if we substitute the former image (
, if we substitute the former image (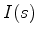 ) with the latter one, we transit from equation 1 to equation 2.
Notice that the new objective function is expressed as a function of only the moveout parameter
) with the latter one, we transit from equation 1 to equation 2.
Notice that the new objective function is expressed as a function of only the moveout parameter 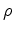 , while the
, while the 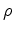 parameter is then related to the model slowness
parameter is then related to the model slowness 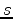 .
.
Furthermore, notice that equation 2 weights the strong-amplitude events more heavily. To make the gradient independent from the strength of reflectors, we further replace 2 with the following semblance objective function:
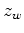 is a local averaging window of length
is a local averaging window of length 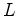 along the depth axis. For the rest of the paper, the summation interval of
along the depth axis. For the rest of the paper, the summation interval of 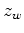 is always
is always
![$ [-L/2,L/2]$](img29.png) ; thus we can safely omit the summation bounds for concise notation.
; thus we can safely omit the summation bounds for concise notation.
We will use gradient-based methods to solve this optimization problem. The gradient given by the objective function 3 is
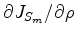 can be easily calculated by taking the derivative along the
can be easily calculated by taking the derivative along the 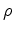 axis of the semblance panel
axis of the semblance panel 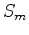 .
.
To evaluate the derivative of the moveout parameter 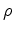 with respect to the slowness model
with respect to the slowness model 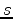 , we define an auxiliary objective function in a fashion similar to the one employed by Luo and Schuster (1991) for cross-well travel-time tomography. The auxiliary objective function is defined for each image point (
, we define an auxiliary objective function in a fashion similar to the one employed by Luo and Schuster (1991) for cross-well travel-time tomography. The auxiliary objective function is defined for each image point (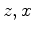 ) as:
) as:
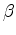 is a simple vertical shift introduced to accommodate bulk shifts in the image introduced by variation in the migration velocity.
Notice that the semblance in objective function 3 is independent of
is a simple vertical shift introduced to accommodate bulk shifts in the image introduced by variation in the migration velocity.
Notice that the semblance in objective function 3 is independent of 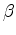 because a bulk shift does not affect the power of the stack; therefore we do not include
because a bulk shift does not affect the power of the stack; therefore we do not include 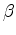 in 3.
in 3.
The explanation for equation 5 is as follows: The moveout parameters
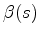 and
and 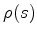 are chosen to describe the kinematic difference between the initial image
are chosen to describe the kinematic difference between the initial image
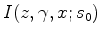 and the new image
and the new image
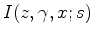 . In other words, if we apply the moveout to the initial image, the resulting image
. In other words, if we apply the moveout to the initial image, the resulting image
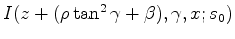 will be the same as the new image
will be the same as the new image
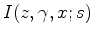 in terms of kinematics; this is indicated by a maximum of the cross-correlation between the two.
in terms of kinematics; this is indicated by a maximum of the cross-correlation between the two.
Given the auxiliary objective function 5,
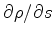 can be found using the rule of partial derivatives for implicit functions.
We compute the gradient of 5 around the maximum at
can be found using the rule of partial derivatives for implicit functions.
We compute the gradient of 5 around the maximum at 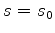 and
and
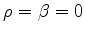 ; consequently
; consequently
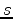 , which gives
, which gives
![$\displaystyle \renewedcommand{arraystretch}{1.5} \left[ \begin{array}{cc} \frac...
...{\partial{J_{\mathrm {aux}}}}{\partial{\beta}\partial{s}} \end{array} \right] .$](img42.png) |
(7) |
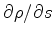 . We denote
. We denote
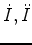 to be the first and second order
to be the first and second order 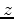 derivatives of image
derivatives of image 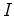 , then define the following:
, then define the following:
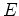 be matrix
be matrix 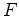 :
:
![$\displaystyle F = \left[ \begin{array}{cc} F_{11} & F_{12} \\ F_{12} & F_{22} \...
...\begin{array}{cc} E_{11} & E_{12} \\ E_{12} & E_{22} \end{array} \right]^{-1}
$](img54.png)
Then
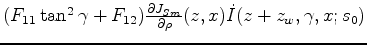 , then we backproject this perturbation to model slowness space using the tomography operator
, then we backproject this perturbation to model slowness space using the tomography operator
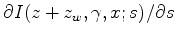 .
.
Since we can compute the gradient in equation 10, any gradient-based optimization method can be used to maximize the objective function defined in equation 3. Nonetheless, in terms of finding the step size, it is more expensive to evaluate equation 3 (which is an approximation of equation 1 purely based on kinematics) than to evaluate the original objective function 1. In our implementation we choose 1 as the maximization goal while using the search direction computed from equation 3.
|
|
|
|
Residual moveout-based wave-equation migration velocity analysis in 3-D |