Recent progress regarding logarithmic Fourier-domain bidirectional deconvolution

No need for preconditioning

Previous time-domain implementations of bidirectional deconvolution (Shen et al. (2011a) and Fu et al. (2011a)) have required preconditioning for both stabilizing the deconvolution result and accelerating the convergence speed. For those methods, we used a prediction error filter (PEF) as our preconditioner. However, using the PEF introduced a polarity change and a time shift problem, because it caused a spike in the first lobe of the Ricker wavelet. However, in the new Fourier-domain method,

$$\begin{split}r_{new} &= FT^{ - 1} (De^{U_{new} } ) \\ &= FT^{... ...ta U} ) \\ &= r * FT^{ - 1} (e^{\alpha \Delta U} ), \end{split}$$ (1)

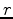where $r$ is the residual, 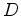$D$ is the data (the uppercase letter indicates a Fourier-domain variable), and 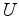$U$ is the logarithmic parameterization of the deconvolution filter.

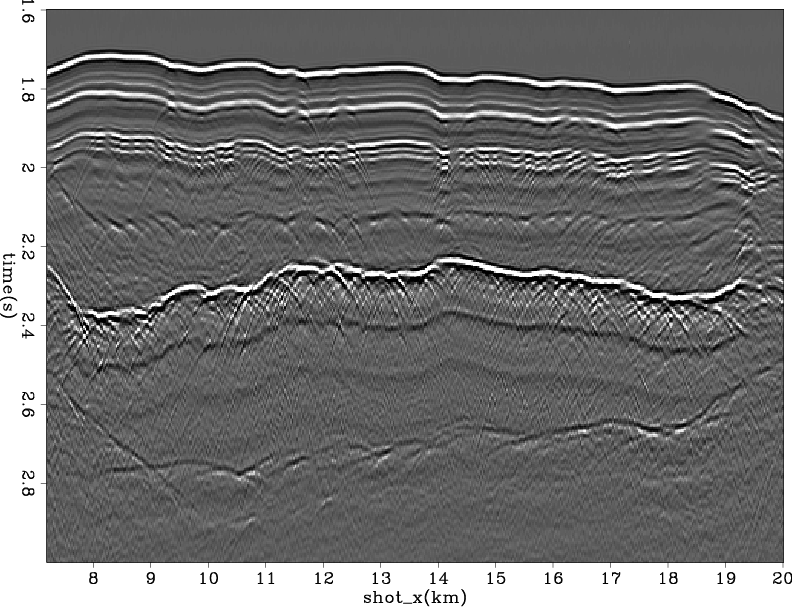
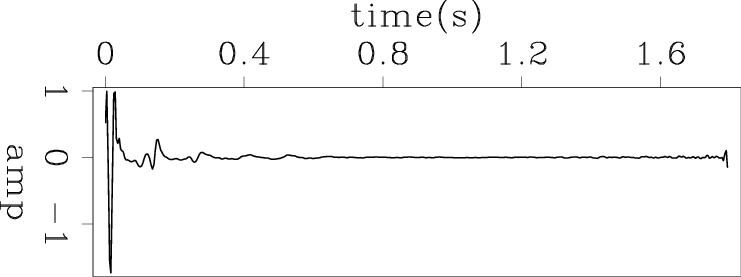
I find that within the iterations, the problem is self-preconditioned. The new update of the $u$ parameter is convolved with the previous residual, so we do not need the PEF preconditioner. Figures 1 through 3 show the comparison between the deconvolution results on a common-offset gather of marine data with and without the PEF preconditioner. In this comparison, I use the 99.5 percentile of all residuals as the threshold for the hyperbolic penalty function. Figure 1 shows the common-offset data gather. Figure 2 shows the deconvolution results with and without the PEF preconditioner. Figure 3 shows the estimated wavelets with and without preconditioning. From this comparison, we can see clearly that the quality of the result without the PEF preconditioner is not inferior to the result with the PEF preconditioner. In addition, the result without the preconditioning avoids the polarity change and time shift. This is caused when the PEF preconditioning introduces an unwelcome initial solution into the deconvolution scheme. This is most obvious in the comparison of the estimated wavelets in Figure 3.

fig-1
Figure 1. A common-offset section of a Gulf of Mexico data set.

fig-2a,fig-2b
Figure 2. Deconvolution results (a) with and (b) without PEF preconditioning.

fig-3a,fig-3b
Figure 3. Estimated wavelets (a) with and (b) without PEF preconditioning.

We found that with slightly different initial solutions or parameters of the deconvolution scheme, we could get quite significantly different results. This could be caused either by the nonlinearity or by the null space of the inversion problem; can not comfirm which is the reason for this phenomenon. Claerbout et al. (2012) claim that the null space may be the major reason, and that therefore a regularization is helpful and may be necessary to solve this problem. However it is still early to draw this conclusion, and more tests are still needed to answer this question.

Recent progress regarding logarithmic Fourier-domain bidirectional deconvolution