Recent progress regarding logarithmic Fourier-domain bidirectional deconvolution

Introduction

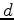Usually, a seismic data trace $d$ can be defined as a convolution of a wavelet 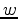$w$ with a reflectivity series 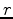$r$ . This can be written as 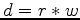$d=r*w$ , where 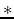$*$ denotes convolution. Blind deconvolution seeks to estimate the wavelet and reflectivity series using only information contained in the data. Previously, seismic blind deconvolution has used two assumptions, namely whiteness and minimum phase. The whiteness assumption supposes that the reflectivity series 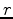$r$ has a flat spectrum, while the minimum-phase assumption supposes that the wavelet 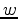$w$ is causal and has a stable inverse. Recently, some new methods have been proposed to limit the effect of these two assumptions in seismic blind deconvolution.

In Zhang and Claerbout (2010a), the authors proposed to use a hyperbolic penalty function introduced in Claerbout (2009) instead of the conventional L2 norm penalty function to solve the blind deconvolution problem. With this method, a sparseness assumption replaces the traditional whiteness assumption. Furthermore, Zhang and Claerbout (2010b) proposed a new method called ``bidirectional deconvolution'' in order to overcome the minimum-phase assumption. Bidirectional deconvolution assumes that any mixed-phase wavelet can be decomposed into a convolution of two parts, 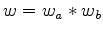$w = w_a*w_b$ , where 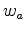$w_a$ is a minimum-phase wavelet and 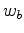$w_b$ is a maximum-phase wavelet. 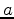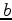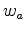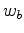To solve this problem, they estimated two deconvolution filters, $a$ and $b$ , which are the inverses of wavelets $w_a$ and $w_b$ , respectively. 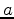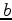Since Zhang and Claerbout (2010b) solved the two deconvolution filters $a$ and $b$ alternately, we call this method the slalom method. Shen et al. (2011a) proposed another method to solve the same problem. They used a linearized approximation to solve the two deconvolution filters simultaneously. We call this method the symmetric method. Fu et al. (2011a) proposed a way to choose an initial solution to overcome the local-minima problem caused by the high nonlinearity of blind deconvolution. Shen et al. (2011b) discussed an important aspect of any inversion problem: preconditioning and how it improves bidirectional deconvolution. All of the aforementioned methods solved the problem in the time domain. Claerbout et al. (2011) proposed a new logarithmic, Fourier-domain, bidirectional deconvolution to solve the same problem. Fu et al. (2011b) showed that this new method converges faster than the above-mentioned time-domain methods

In this paper, I will attempt to answer an important question: Should we use a preconditioner with the logarithmic Fourier-domain bidirectional deconvolution? I will then show an example of including a gain function in this method.

Recent progress regarding logarithmic Fourier-domain bidirectional deconvolution