|
|
|
|
Anisotropic tomography with rock physics constraints |
|
AcquiGeo
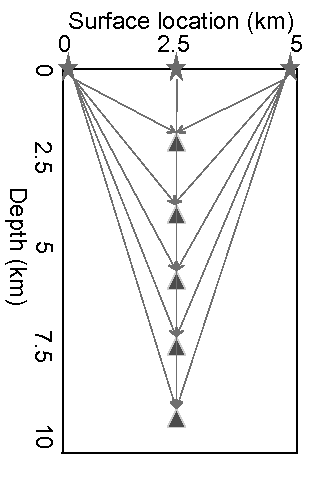
Figure 2. Walkaway VSP acquisition geometry. |
|
|---|---|
|
|
Two 1.5D models are evaluated using this method. One is a shale (sandy shale) model which completely follows the covariance matrix we generated from the rock physics modeling; the other is the same except for a layer of isotropic sand where the prior information is ``wrong''.
Now we are ready to test our method using different prior information. For different tests, we apply the same smoothing operator
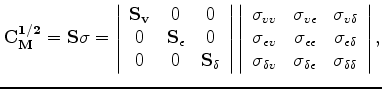 , but different estimates of point-by-point cross-parameter covariance
, but different estimates of point-by-point cross-parameter covariance
![]() . In the notations below, ``no prior'' means
. In the notations below, ``no prior'' means
![]() ; ``column weighting'' means
; ``column weighting'' means
![]() has only diagonal elements which are constant for every grid point in the subsurface; ``diagonal covariance'' means
has only diagonal elements which are constant for every grid point in the subsurface; ``diagonal covariance'' means
![]() has only diagonal elements which vary according to the rock physics modeling results; ``full covariance'' means
has only diagonal elements which vary according to the rock physics modeling results; ``full covariance'' means
![]() has all nine elements which vary according to the rock physics prior for each grid point in the subsurface.
has all nine elements which vary according to the rock physics prior for each grid point in the subsurface.
|
|---|
|
model1
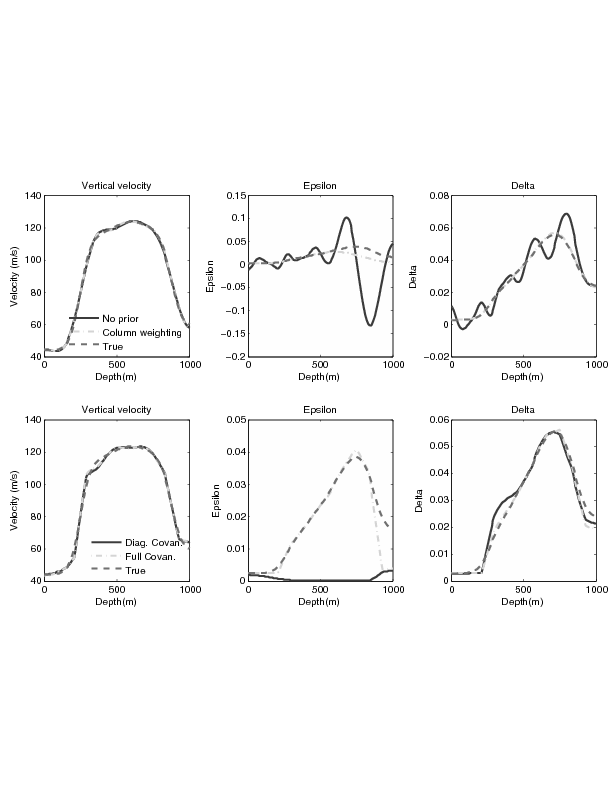
Figure 3. Inversion results of the shale (sandy shale) model. Panels on the left show the velocity perturbation, in the middle |
|
|
Figure 3 shows the inversion results of the shale (sandy shale) model. It is obvious that vertical velocity is the best constrained variable, therefore, all inversion schemes yield good estimations for vertical velocity. However, instability is seen in the results of ![]() and
and ![]() when no prior information is included. The oscillations in
when no prior information is included. The oscillations in ![]() and
and ![]() are out-of-phase, which is the numerical proof for the theoretical predicted trade-off between these two parameters. Inversion with column weighting yields more stable results for
are out-of-phase, which is the numerical proof for the theoretical predicted trade-off between these two parameters. Inversion with column weighting yields more stable results for ![]() and the shallow part of
and the shallow part of ![]() . For the deeper part and also less constrained part of
. For the deeper part and also less constrained part of ![]() , column weighting gives a less satisfactory result. When rock physics prior knowledge is introduced, the inversion is further stabilized. Both the diagonal and the full covariance give good estimations for velocity and
, column weighting gives a less satisfactory result. When rock physics prior knowledge is introduced, the inversion is further stabilized. Both the diagonal and the full covariance give good estimations for velocity and ![]() , while superior result for
, while superior result for ![]() is obtained by full covariance since correct prior knowledge adds information to the inversion. The fact that a much closer estimation for
is obtained by full covariance since correct prior knowledge adds information to the inversion. The fact that a much closer estimation for ![]() was produced using full covariance rather than the diagonal one suggests that large cross-terms exist in the covariance matrix.
was produced using full covariance rather than the diagonal one suggests that large cross-terms exist in the covariance matrix.
|
|---|
|
model2
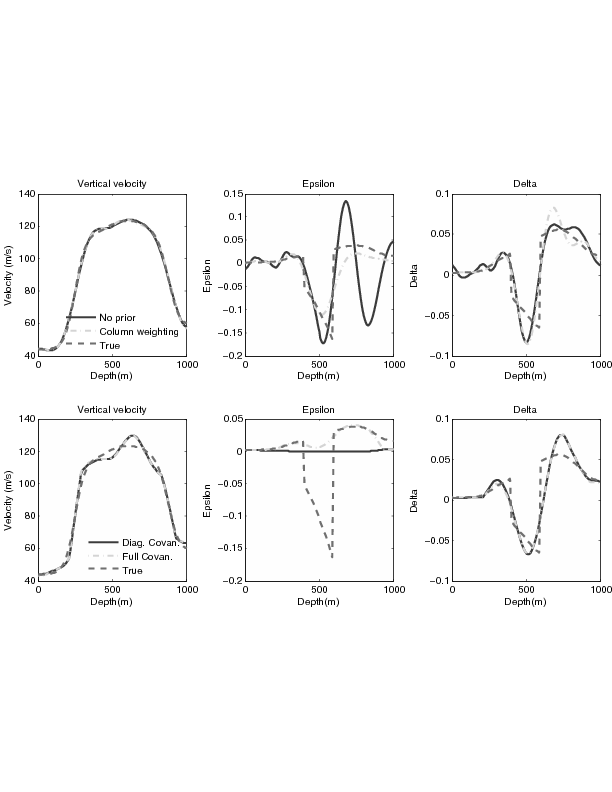
Figure 4. Inversion results of the shale model with an isotropic sand layer. Panels are arranged in the same order as Figure 3. |
|
|
Figure 4 shows the inversion results of the shale (sandy shale) model with an isotropic layer in the middle. Similar stability conclusions can be drawn as for the shale (sandy shale) case. Notice that for the well-constrained variable ![]() , inversion is able to resolve the isotropic layer even though ``wrong'' prior information is provided. However, the inversion result is highly biased towards the prior information for
, inversion is able to resolve the isotropic layer even though ``wrong'' prior information is provided. However, the inversion result is highly biased towards the prior information for ![]() where it is not so well constrained.
where it is not so well constrained.
|
|
|
|
Anisotropic tomography with rock physics constraints |