Suppressing wraparound artifacts of the Fourier method

The periodic boundary conditions both in the squared time $\sigma$ and the spatial coordinate x, implied by the Fourier approach, are artificial in the problem of velocity continuation. The artificial periodicity is convenient from the computational point of view. However, false periodic events (wraparound artifacts) should be suppressed in the final output. A natural method for attacking this problem is to apply zero padding in the physical space prior to Fourier transform. Of course, this method involves an additional expense of the grid size increase.

 

fft-imp
Figure 5 Impulse responses (Green's functions) of velocity continuation, computed by the Fourier method. Top: without zero padding, bottom: with zero padding. The left plots correspond to continuation to a larger velocity (+1 km/sec); the right plots, smaller velocity, (-1 km/sec).

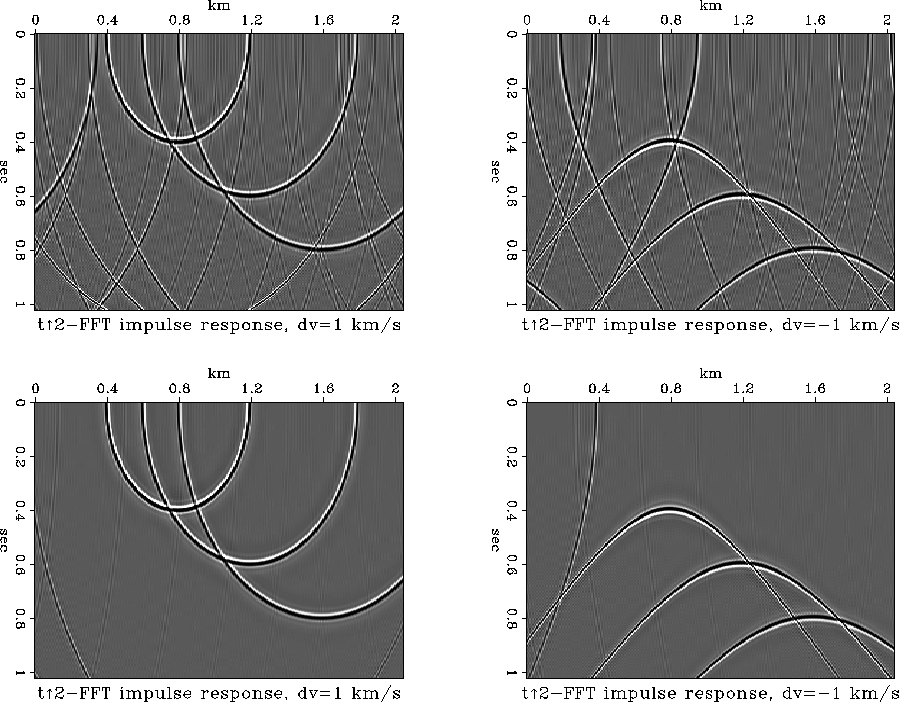The top plots in Figure 5 show the numerical impulse responses of velocity continuation, computed by the Fourier method. The initial data contained three spikes, passed through a narrow-band filter. Theoretically, continuation to larger velocity (the left plot) should create three elliptical wavefronts, and continuation to smaller velocity (right plot) should create three hyperbolic wavefronts (Rothman et al. , 1985). We can see that the results are largely contaminated with wraparound artifacts. The result of applying zero padding (the bottom plots in Figure 5) shows most of the artifacts suppressed.

Chebyshev spectral method, discussed in the next section, provides a spectral accuracy while dealing correctly with non-periodic data.