




Next: Dynamics of Residual DMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: Dynamics of Zero-Offset Velocity
According to the theory of characteristics, described in the beginning
of this section, the kinematic residual NMO equation
(22) corresponds to the dynamic equation of the form
| 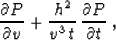 |
(58) |
whose general solution is easily found to be
| 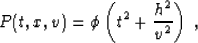 |
(59) |
where 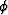 is an arbitrary smooth function.
The combination of dynamic equations (58) and
(55) leads to an approximate prestack velocity
continuation with the residual DMO effect neglected. To accomplish the
combination, we can simply add the term
is an arbitrary smooth function.
The combination of dynamic equations (58) and
(55) leads to an approximate prestack velocity
continuation with the residual DMO effect neglected. To accomplish the
combination, we can simply add the term 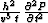 to the left-hand
side of equation (55). This addition changes the
kinematics of velocity continuation, but doesn't change the amplitude
properties embedded in the transport equation (56).
to the left-hand
side of equation (55). This addition changes the
kinematics of velocity continuation, but doesn't change the amplitude
properties embedded in the transport equation (56).





Next: Dynamics of Residual DMO
Up: FROM KINEMATICS TO DYNAMICS
Previous: Dynamics of Zero-Offset Velocity
Stanford Exploration Project
9/12/2000