




Next: FINITE-DIFFERENCING POST-STACK VELOCITY CONTINUATION
Up: Fomel: Velocity continuation
Previous: DERIVING THE KINEMATIC EQUATIONS
The goal of this appendix is to prove the equivalence between the
result of the zero-offset velocity continuation from zero velocity and
the conventional post-stack migration. After solving the velocity
continuation problem in the frequency domain, I transform the
solution back to the time-and-space domain and compare it with the
famous Kirchhoff migration operator.
Zero-offset migration based on velocity continuation is the solution
of the boundary problem for equation (55) with the
boundary condition
| 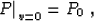 |
(82) |
where P0(t0,x0) is the zero-offset seismic section, and
P(t,x,v) is the continued wavefield. In order to find the solution
of the boundary problem composed of (55) and (82), it is
convenient to apply the function transformation 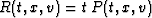 , the time coordinate transformation
, the time coordinate transformation 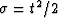 , and,
finally, the double Fourier transform over the squared time coordinate
, and,
finally, the double Fourier transform over the squared time coordinate
 and the spatial coordinate x:
and the spatial coordinate x:
| 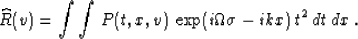 |
(83) |
With the change of domain, equation (55) transforms
to the ordinary differential equation
| 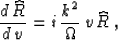 |
(84) |
and the boundary condition (82) transforms to the initial
value condition
| 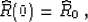 |
(85) |
where
| 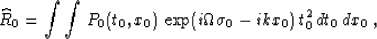 |
(86) |
and 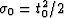 . The unique solution of the initial value
(Cauchy) problem (84) - (85) is easily found to be
. The unique solution of the initial value
(Cauchy) problem (84) - (85) is easily found to be
| 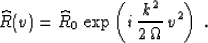 |
(87) |
We can see that, in the transformed domain, velocity continuation is a
unitary phase-shift operator. An immediate consequence of this
remarkable fact is the cascaded migration decomposition of post-stack
migration Larner and Beasley (1987):
| 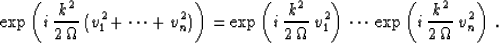 |
(88) |
Analogously, three-dimensional post-stack migration is decomposed
into the two-pass procedure Jakubowicz and Levin (1983):
| 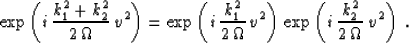 |
(89) |
The inverse double Fourier transform of both sides of equality
(87) yields the integral (convolution) operator
| 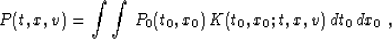 |
(90) |
with the kernel K defined by
| 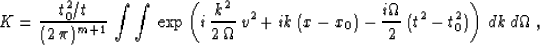 |
(91) |
where m is the number of dimensions in x and k (m equals 1
or 2). The inner integral on the wavenumber axis k in formula
(91) is a known table integral Gradshtein and Ryzhik (1994). Evaluating this
integral simplifies equation (91) to the form
| ![\begin{displaymath}
K = {{t_0^2/t} \over {(2\,\pi)^{m/2+1}\,v^m}}\,
\int\,(i\Ome...
...^2 - t^2 - {{(x - x_0)^2} \over v^2}\right)\right]\,
d\Omega\;.\end{displaymath}](img132.gif) |
(92) |
The term 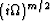 is the spectrum of the anti-causal
derivative operator
is the spectrum of the anti-causal
derivative operator 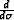 of the order m/2. Noting
the equivalence
of the order m/2. Noting
the equivalence
| 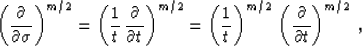 |
(93) |
which is exact in the 3-D case (m=2) and asymptotically correct in
the 2-D case (m=1), and applying the convolution theorem, we can
transform operator (90) to the form
| 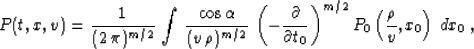 |
(94) |
where 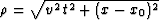 , and
, and 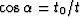 . Operator (94) coincides with the Kirchhoff operator
of the conventional post-stack time migration Schneider (1978).
. Operator (94) coincides with the Kirchhoff operator
of the conventional post-stack time migration Schneider (1978).
C





Next: FINITE-DIFFERENCING POST-STACK VELOCITY CONTINUATION
Up: Fomel: Velocity continuation
Previous: DERIVING THE KINEMATIC EQUATIONS
Stanford Exploration Project
9/12/2000