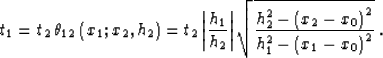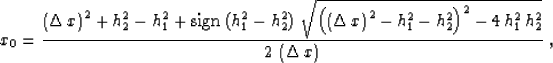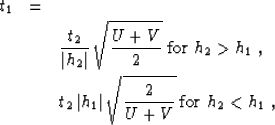Next: AMO APERTURE: CASCADING MIGRATION
Up: Fomel & Biondi: t-x
Previous: Introduction
In this section, we present a new version of the AMO derivation.
Since
the entire derivation is performed in the time-space domain, it is more
straightforward than the stationary phase technique developed for the
same purpose by Biondi and Chemingui 1994.
Let 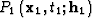 be the input of an AMO
operator (common-azimuth and common-offset seismic
reflection data after normal moveout correction) and
be the input of an AMO
operator (common-azimuth and common-offset seismic
reflection data after normal moveout correction) and
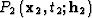 be the output. Here
be the output. Here
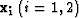 are midpoint locations on the surface:
are midpoint locations on the surface:
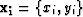 , and
, and
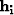 are half-offset vectors.
The 3-D AMO operator has the following general form:
are half-offset vectors.
The 3-D AMO operator has the following general form:
| 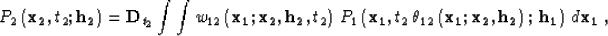 |
(1) |
where 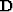 is the differentiation operator
is the differentiation operator 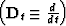 ,
, 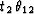 is the summation
path, and w12 is the weighting function. In this section we will
evaluate
is the summation
path, and w12 is the weighting function. In this section we will
evaluate 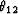 and w12 using the cascade of integral 3-D DMO and
inverse DMO operators in the time-space domain. The idea of this
derivation originated in Biondi and Chemingui's paper
1994, where it was
applied with the frequency-domain DMO and inverse DMO operators. In
the next section,
we apply a new geometric approach to evaluate the AMO aperture (range of
integration in (1)).
and w12 using the cascade of integral 3-D DMO and
inverse DMO operators in the time-space domain. The idea of this
derivation originated in Biondi and Chemingui's paper
1994, where it was
applied with the frequency-domain DMO and inverse DMO operators. In
the next section,
we apply a new geometric approach to evaluate the AMO aperture (range of
integration in (1)).
To derive (1) in the time-space domain,
an integral
(Kirchoff-type) DMO operator of the form
| 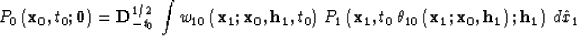 |
(2) |
is cascaded with an inverse DMO of the form
| 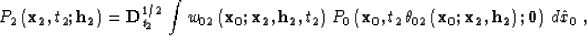 |
(3) |
where 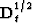 stands for the operator of half-order differentiation
(equivalent to
stands for the operator of half-order differentiation
(equivalent to 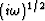 multiplication in Fourier domain),
multiplication in Fourier domain),
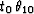 and
and 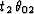 are the summation paths of
the DMO and inverse DMO
operators Deregowski and Rocca (1981):
are the summation paths of
the DMO and inverse DMO
operators Deregowski and Rocca (1981):
| 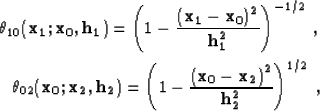 |
(4) |
| (5) |
w10 and w02 are the corresponding weighting functions (amplitudes of
impulse responses), 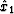 is the component of
is the component of 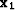 along the
along the
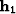 azimuth, and
azimuth, and 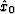 is the component of
is the component of 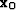 along the
along the
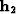 azimuth.
Integral operators (2) and (3) correspond to
the high-frequency asymptotic (the geometrical seismic) description of
the wave field. As shown by Stovas and Fomel 1993,
operator (3) has an asymptotically equivalent
form
azimuth.
Integral operators (2) and (3) correspond to
the high-frequency asymptotic (the geometrical seismic) description of
the wave field. As shown by Stovas and Fomel 1993,
operator (3) has an asymptotically equivalent
form
| 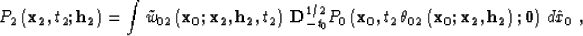 |
(6) |
where 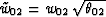 .
.
Both DMO and inverse DMO operate on 3-D seismic data
as 2-D operators, since their apertures are defined on a line. This
implies that for a given input midpoint 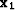 , the corresponding
location of
, the corresponding
location of 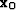 must belong to the
line going through
must belong to the
line going through 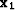 , with the azimuth defined by the input
offset
, with the azimuth defined by the input
offset 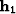 .
Similarly,
.
Similarly, 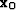 must be on the line going through
must be on the line going through
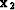 with the azimuth of
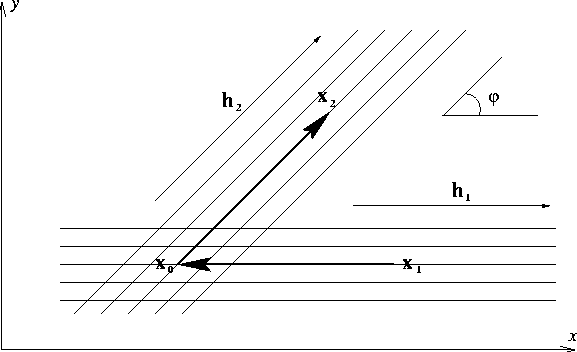
with the azimuth of 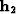 (Figure 1).
These theoretical facts lead us to the following conclusion:
(Figure 1).
These theoretical facts lead us to the following conclusion:
For a given pair of input and output midpoints 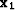 and
and 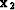 of the AMO operator, the corresponding midpoint
of the AMO operator, the corresponding midpoint 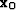 on
the intermediate zero-offset gather is determined by the intersection of
two lines drawn
through
on
the intermediate zero-offset gather is determined by the intersection of
two lines drawn
through 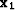 and
and 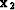 in the offset directions.
in the offset directions.
Applying the geometric connection among the three midpoints, we can
find the cascade
of the DMO
and inverse DMO operators in one step.
For this purpose, it is convenient to choose an orthogonal coordinate
system 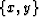 on the
surface in such a way that the direction of the x axis corresponds
to the input azimuth
(Figure 1).
In this case the connection between the three midpoints is given by
on the
surface in such a way that the direction of the x axis corresponds
to the input azimuth
(Figure 1).
In this case the connection between the three midpoints is given by
| 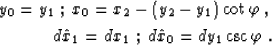 |
(7) |
| (8) |
amox12
Figure 1 Geometric
relationships between input and output midpoint locations in AMO.

Substituting (2) into (6) and taking into account
(8) produces the 3-D integral AMO operator (1),
where
| 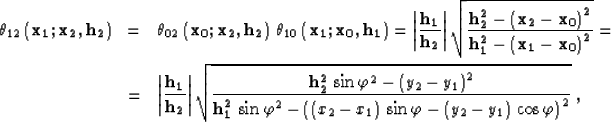 |
|
| (9) |
| 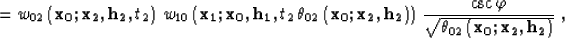 |
(10) |
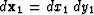 . Equation
. Equation
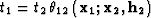 is the same
as equation (4) in Biondi and Chemingui (1994) except for a different
notation. The weighting function of the derived AMO operator
is the same
as equation (4) in Biondi and Chemingui (1994) except for a different
notation. The weighting function of the derived AMO operator
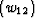 depends on the weighting functions of DMO and inverse DMO that are involved in
the construction. In Appendix A, we apply equation (10) to two
popular versions of the DMO weighting functions that
correspond to Hale's 1984 and Zhang's
1988 DMO operators.
depends on the weighting functions of DMO and inverse DMO that are involved in
the construction. In Appendix A, we apply equation (10) to two
popular versions of the DMO weighting functions that
correspond to Hale's 1984 and Zhang's
1988 DMO operators.
Deriving formula (9), we have to assume
that the input
and output offset azimuths are different (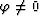 ). In the case
of equal azimuths, AMO reduces to 2-D offset continuation (OC). The
location of
). In the case
of equal azimuths, AMO reduces to 2-D offset continuation (OC). The
location of 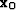 in this case is not constrained by the input
and output midpoints and can take different values on the line.
Therefore the superposition of DMO and inverse DMO for offset
continuation is a convolution on that line. To find the summation path
of the OC operator, we should consider the envelope of the family of traveltime
curves (where x0 is the parameter of a curve in the family):
in this case is not constrained by the input
and output midpoints and can take different values on the line.
Therefore the superposition of DMO and inverse DMO for offset
continuation is a convolution on that line. To find the summation path
of the OC operator, we should consider the envelope of the family of traveltime
curves (where x0 is the parameter of a curve in the family):
| 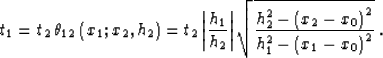 |
(11) |
Solving the envelope condition
| 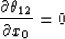 |
(12) |
with respect to x0 produces
| 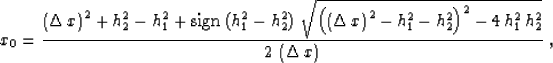 |
(13) |
where 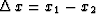 .Substituting (13) into (11), we get the explicit
expression of the OC summation path:
.Substituting (13) into (11), we get the explicit
expression of the OC summation path:
| 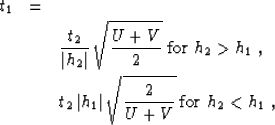 |
|
| |
| (14) |
where 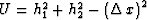 , and
, and
 .Equation (14) corresponds to formula (6) in
Biondi and Chemingui (1994) (with a typo corrected). The same
expression was obtained in a different way by Stovas and Fomel
1993.
The apparent difference between the 2-D and 3-D solutions introduces the
problem of finding a consistent description valid for both cases.
Such a description is especially important for practical applications
dealing with small angles of azimuth rotation, e.g. cable feather
correction in marine seismics. The next section develops
a way of solving
this problem, which
refers to the kinematic theory of AMO and follows the ideas that
Deregowski and Rocca 1981 applied
to DMO-type operators.
.Equation (14) corresponds to formula (6) in
Biondi and Chemingui (1994) (with a typo corrected). The same
expression was obtained in a different way by Stovas and Fomel
1993.
The apparent difference between the 2-D and 3-D solutions introduces the
problem of finding a consistent description valid for both cases.
Such a description is especially important for practical applications
dealing with small angles of azimuth rotation, e.g. cable feather
correction in marine seismics. The next section develops
a way of solving
this problem, which
refers to the kinematic theory of AMO and follows the ideas that
Deregowski and Rocca 1981 applied
to DMO-type operators.





Next: AMO APERTURE: CASCADING MIGRATION
Up: Fomel & Biondi: t-x
Previous: Introduction
Stanford Exploration Project
9/12/2000
![]() be the input of an AMO
operator (common-azimuth and common-offset seismic
reflection data after normal moveout correction) and
be the input of an AMO
operator (common-azimuth and common-offset seismic
reflection data after normal moveout correction) and
![]() be the output. Here
be the output. Here
![]() are midpoint locations on the surface:
are midpoint locations on the surface:
![]() , and
, and
![]() are half-offset vectors.
The 3-D AMO operator has the following general form:
are half-offset vectors.
The 3-D AMO operator has the following general form:
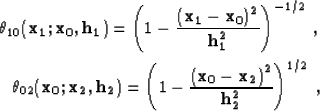
![]() , the corresponding
location of
, the corresponding
location of ![]() must belong to the
line going through
must belong to the
line going through ![]() , with the azimuth defined by the input
offset
, with the azimuth defined by the input
offset ![]() .
Similarly,
.
Similarly, ![]() must be on the line going through
must be on the line going through
![]() with the azimuth of
with the azimuth of ![]() (Figure 1).
These theoretical facts lead us to the following conclusion:
(Figure 1).
These theoretical facts lead us to the following conclusion:
and
of the AMO operator, the corresponding midpoint
on the intermediate zero-offset gather is determined by the intersection of two lines drawn through
and
in the offset directions.
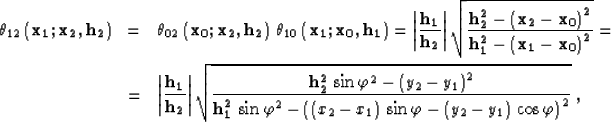
![]() ). In the case
of equal azimuths, AMO reduces to 2-D offset continuation (OC). The
location of
). In the case
of equal azimuths, AMO reduces to 2-D offset continuation (OC). The
location of ![]() in this case is not constrained by the input
and output midpoints and can take different values on the line.
Therefore the superposition of DMO and inverse DMO for offset
continuation is a convolution on that line. To find the summation path
of the OC operator, we should consider the envelope of the family of traveltime
curves (where x0 is the parameter of a curve in the family):
in this case is not constrained by the input
and output midpoints and can take different values on the line.
Therefore the superposition of DMO and inverse DMO for offset
continuation is a convolution on that line. To find the summation path
of the OC operator, we should consider the envelope of the family of traveltime
curves (where x0 is the parameter of a curve in the family):