ISOTROPIC HETEROGENEITY VERSUS ANELLIPTIC ANISOTROPY

A controversial issue associated with the topic of this paper is whether the non-hyperbolicity of the traveltime curves is caused mainly by heterogeneity or by anisotropy. To find a connection between the two different descriptions of media, we can consider an alternative three-parameter traveltime approximation (the anelliptic anisotropic moveout formula), proposed by Muir and Dellinger 1985 :  

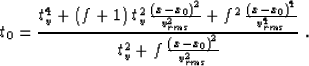$$t_0 = {{t_v^4+(f+1)\,t_v^2\,{\left(x-x_0\right)^2 \over v_{r... ...}} \over {t_v^2+f\,{\left(x-x_0\right)^2 \over v_{rms}^2}}}\;.$$ (32)

Here f is the parameter of anellipticity. Differentiating (32) four times, setting l=x-x₀ to zero, and equating the result with (20) results in the following formal relationship between f and Malovichko's parameter of heterogeneity:  

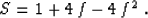$$S = 1 + 4\,f - 4\,f^2\;.$$ (33)

Equation (33) clearly demonstrates the uncertainty between the anisotropic and heterogeneous isotropic interpretations. Both of them can explain the cause of the nonhyperbolicity of traveltime curves. An important difference is that the parameter of heterogeneity is uniquely determined by the velocity distribution according to (15), while the f parameter is assumed to be an independent functional. The definition (15), applied in combination with (24), is suitable for calculating the Stolt stretch factor in an isotropic model for a given velocity function. If the correction parameter is measured experimentally by a non-hyperbolic velocity analysis in the form of either equation (13) or equation (32), it accumulates both heterogeneous and anisotropic factors and can be used for an explicit determination of W in (24) independently of the preferred explanation. In the case of the anisotropic moveout velocity analysis, we merely need to substitute the connection formula (33) into (24) to find W. An alternative approach to Stolt-type migration in transversally isotropic media was proposed recently by Ecker and Muir 1993. However, Stolt stretch migration is superior to that method in its ability to cope with varying rms velocities.