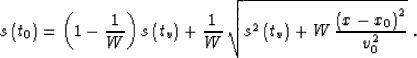Next: EVALUATING THE W PARAMETER
Up: Fomel: Stolt stretch
Previous: Introduction
In order to simplify the references, I will begin with the textbook
definitions of
the Stolt migration
method. The reader familiar with Stolt stretch theory can skip this
section and go on to
a new piece of theory in the next one.
Post-stack seismic migration is theoretically a two-stage process
consisting of wavefield downward continuation in depth z based on
the wave equation
| 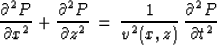 |
(1) |
and the imaging condition t=0 (here the velocity v is twice as
small as
the actual wave velocity).
Stolt time migration performs both stages in one step, applying the
frequency-domain
operator
| 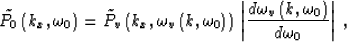 |
(2) |
where
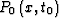 stands for the initial zero-offset (stacked)
seismic
section defined on the surface z=0,
stands for the initial zero-offset (stacked)
seismic
section defined on the surface z=0,
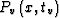 is the time-migrated section, and tv is
the vertical traveltime
is the time-migrated section, and tv is
the vertical traveltime
| 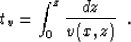 |
(3) |
The function
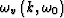 in (2) corresponds to the dispersion
relation of
the wave equation (1) and in the constant velocity case has the explicit
expression
in (2) corresponds to the dispersion
relation of
the wave equation (1) and in the constant velocity case has the explicit
expression
| 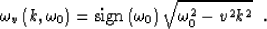 |
(4) |
The choice of the sign in (4) is essential to distinguish
between
upgoing and downgoing waves. It is the upgoing part of the wave field
that is used in migration.
For the case of a varying velocity Stolt 1978
suggested the following change
of the time variable (referred to in the literature as Stolt stretch):
| 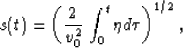 |
(5) |
where v0 is an arbitrarily chosen constant velocity, and  is a
function defined by the parametric expressions
is a
function defined by the parametric expressions
| 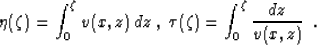 |
(6) |
With the stretch (5), seismic time migration can be
related to the transformed wave equation
| 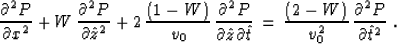 |
(7) |
Here 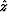 and
and 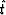 are the transformed depth and time coordinates that
possess
the following property: if
are the transformed depth and time coordinates that
possess
the following property: if 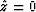 ,
, 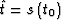 , and if
, and if
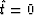 ,
, 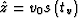 . W is a varying
coefficient defined as
. W is a varying
coefficient defined as
| 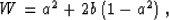 |
(8) |
where
Stolt's idea was to replace the slowly varying parameter W with its average
value.
Thus equation (7) is approximated by an equation with constant
coefficients, which has the dispersion relation
| 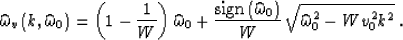 |
(9) |
Stolt's approximate method for migration in heterogeneous media consists of the
following steps:
- 1.
- stretching the time variable according to (5),
- 2.
- interpolating the stretched time to a regular grid,
- 3.
- double Fourier transform,
- 4.
- f-k time migration by operator (2) with the dispersion
relation
(9),
- 5.
- inverse Fourier transform,
- 6.
- inverse stretching (shrinking) the vertical time variable on the migrated
section.
The value of W must be chosen prior to migration. According to
Stolt's original definition (8),
the depth variable z gradually changes in the migration process from
zero to 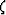 , causing the coefficient
b in (8) to change monotonically from 0 to 1. If the velocity v
monotonically increases with depth, then
, causing the coefficient
b in (8) to change monotonically from 0 to 1. If the velocity v
monotonically increases with depth, then
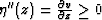 , and the average value of b is
, and the average value of b is
| 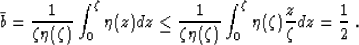 |
(10) |
As follows from (8) and (10), in the case of monotonically
increasing
velocity, the average value of W has to be less than 1 (W equals 1 in a
constant
velocity case). Analogously, in the case of a monotonically decreasing
velocity, W is always greater than 1.
In practice, W is included in migration routines as a
user-defined
parameter, and its value is usually chosen to be somewhere in the
range of 1/2 to 1.
In this
paper I will describe a straightforward way to determine the most
appropriate value of W for a given velocity distribution.
A useful tool for that purpose is Stewart Levin's formula for the
traveltime curve. Levin 1985 applied the
stationary phase technique
to the dispersion relation (9) to obtain an explicit formula for
the
summation curve of the integral migration operator analogous to the
Stolt stretch
migration. The formula evaluates the summation path in the stretched
coordinate system, as follows:
| 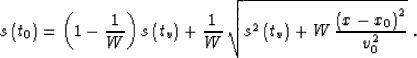 |
(11) |
Here x0 is the midpoint location on a zero-offset seismic section,
and x is the
space coordinate on the migrated section.
Formula (11) shows that, with the stretch of the time coordinate, the
summation curve has the
shape of a hyperbola with the apex at 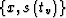 and
the center (the intersection of the asymptotes) at
and
the center (the intersection of the asymptotes) at
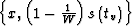 . In the case
of homogeneous media, W=1,
. In the case
of homogeneous media, W=1, 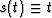 , and (11) reduces to the
well-known
hyperbolic diffraction traveltime curve. It is interesting to note
that inverting formula (11) for
, and (11) reduces to the
well-known
hyperbolic diffraction traveltime curve. It is interesting to note
that inverting formula (11) for 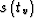 determines
the impulse response of the migration operator, which can be
interpreted as
the wavefront from a point source in the
determines
the impulse response of the migration operator, which can be
interpreted as
the wavefront from a point source in the
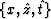 domain of equation
(7):
domain of equation
(7):
| 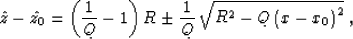 |
(12) |
where 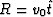 , and Q=2-W.
According to equation (12), wavefronts from a point source in
the stretched
coordinates
for W<2 have an elliptic shape, with the center of the ellipse
at
, and Q=2-W.
According to equation (12), wavefronts from a point source in
the stretched
coordinates
for W<2 have an elliptic shape, with the center of the ellipse
at
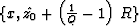 and the semi-axes
and the semi-axes
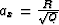 and
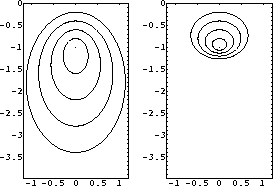
and 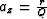 . The ellipses stretch
differently for W<1 and W>1 (Figure 1). In the upper part
that corresponds to the upgoing waves, they look nearly spherical, since
the radius of the front curvature at the top apex equals the distance from the
source.
. The ellipses stretch
differently for W<1 and W>1 (Figure 1). In the upper part
that corresponds to the upgoing waves, they look nearly spherical, since
the radius of the front curvature at the top apex equals the distance from the
source.
stofro
Figure 1 Wavefronts from a point source
in the stretched coordinate system. Left: velocity decreases with
depth (W=1.5). Right: velocity increases with depth (W=0.5).
|
|  |










Next: EVALUATING THE W PARAMETER
Up: Fomel: Stolt stretch
Previous: Introduction
Stanford Exploration Project
4/19/2000