 |
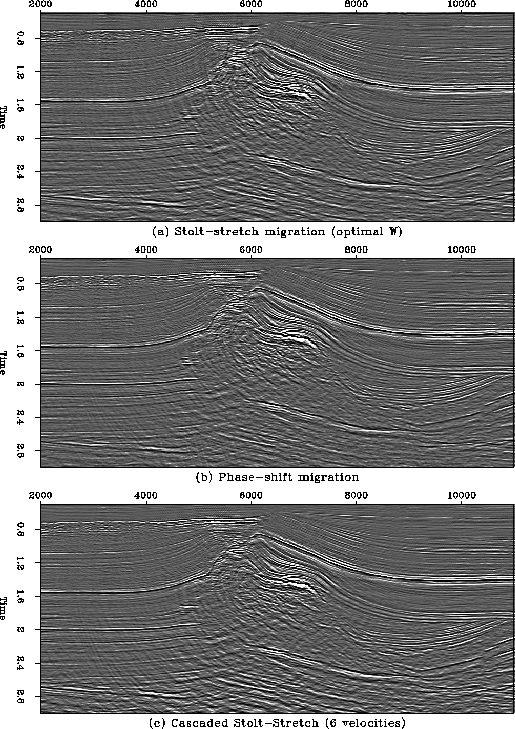
Figure 1 (a) Section of the North Sea data, after NMO-stack. (b) Section migrated using Stolt's method with v0=2000 m/s. (c) Section migrated using Stolt-stretch with an arbitrary value W=0.5 for the paramater of heterogeneity.
Following the study by Larner et al. 1989, we selected a dataset that includes steep dips in order to test the accuracy of our algorithms. The data is courtesy of Elf Aquitaine, was recorded in the North Sea, and shows a salt dome (Figure 3). Figure 1 shows (a) the data after NMO-stack and (b) after poststack Stolt migration, using a constant velocity of 2000 m/s. We notice that Stolt's method obviously yields undermigrated events on both sides of the salt body. Using a higher velocity to focus them better would have created overmigration artifacts at shallow reflectors. Stolt-stretch migrated section (c) using W=0.5 should be compared with figure 2a.
Using the Stolt-stretch method with the optimal choice for W derived from equation (9) yields a better focusing of events at all depths (Figure 2a), compared to other values of W (Figures 1b and 1c, respectively for W equals 1.0 and 0.5). The v(z) model used for migration is shown in Figure 4a and was obtained by averaging laterally the reference velocity model.
 |
 |
 |
The reference method of migration for our study is the phase-shift
approach proposed by Gazgag 1978. It is
known to be perfectly accurate for all dips up to ![]() in a
v(z) velocity field. A comparison between the phase-shift migration
result (Figure 2b) and the section migrated
with the Stolt-stretch approach shows almost no difference for flat
events. However, a more detailed analysis reveals significant errors
for steep events inside and around the salt body. The approximation
made by stretching the time axis breaks for recovering steep events.
in a
v(z) velocity field. A comparison between the phase-shift migration
result (Figure 2b) and the section migrated
with the Stolt-stretch approach shows almost no difference for flat
events. However, a more detailed analysis reveals significant errors
for steep events inside and around the salt body. The approximation
made by stretching the time axis breaks for recovering steep events.
A way to overcome the difficulties encountered by Stolt's migration is
to divide the whole process into a cascade, as suggested by Beasley et
al. 1988. The theory of cascaded migration
proves that f-k migration algorithms with a v(t) velocity model
like Stolt-stretch can be performed sequentially as a cascade of n
migrations with smaller interval velocities ![]() ,such as
,such as ![]() . At a given vertical
traveltime t, all the successive velocity models have to be
constant, except the last one Larner and Beasley (1987). Typically, the
first stage is done with a constant velocity model and can be computed
using Stolt's algorithm, which is then accurate for all
dips. Figure 4 illustrates such a cascade of
velocity models in our
particular case, with 3 and 6 stages.
. At a given vertical
traveltime t, all the successive velocity models have to be
constant, except the last one Larner and Beasley (1987). Typically, the
first stage is done with a constant velocity model and can be computed
using Stolt's algorithm, which is then accurate for all
dips. Figure 4 illustrates such a cascade of
velocity models in our
particular case, with 3 and 6 stages.
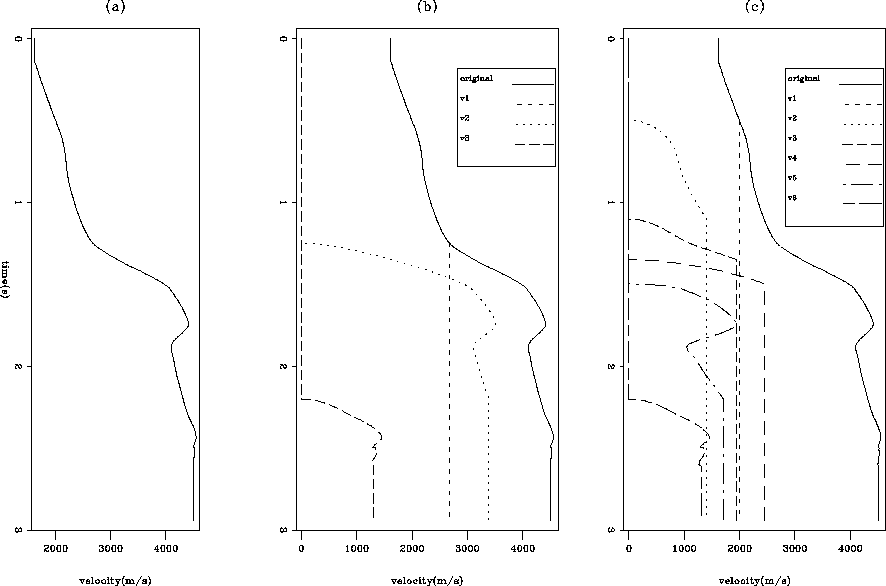 |
As a consequence of this decomposition, each intermediate velocity model shows not only a smaller velocity but also less vertical heterogeneity. In other words, the Stolt-stretch parameter W estimated for each stage tends to be closer to 1.0, thus reducing the migration errors due to the approximation. Figure 2c shows the migration result using a 6-stage cascaded scheme. All the successive values of W were greater than 0.8. There are almost no differences with the phase-shift result (Figure 2b).