




Next: REFERENCES
Up: Clapp, et al.: Steering
Previous: REGULARIZATION
We show that by using helicon enabled inverse
operators built from small steering filters we can quickly obtain esthetically
pleasing models.
Tests on smooth models, with a single dip at each location proved
successful. The methodology does not adequately handle models with
multiple dips at each location and presupposes some knowledge of the
desired final model.
A different approach would be to estimate
the steering filters (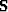 ) from the experimental data (
) from the experimental data ( ).
Generally, this leads to a
system of non-linear equations
).
Generally, this leads to a
system of non-linear equations
| 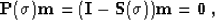 |
(24) |
which need to be solved with respect to  . One way of solving
system (24) is to apply the general Newton's method,
which leads to the iteration
. One way of solving
system (24) is to apply the general Newton's method,
which leads to the iteration
| 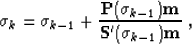 |
(25) |
where the derivative 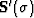 can be computed analytically.
It is interesting to note that if we start with
can be computed analytically.
It is interesting to note that if we start with 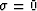 and apply
the first-order filter (8), then the first iteration of
scheme (25) will be exactly equivalent to the
slope-estimation method of Claerbout (1992a), used by
Bednar (1997) for calculating coherency attributes.
Finally, the steering filter
regularization methodology needs to be tried in
conjunction with a variety of operators and
applied to real data problems.
and apply
the first-order filter (8), then the first iteration of
scheme (25) will be exactly equivalent to the
slope-estimation method of Claerbout (1992a), used by
Bednar (1997) for calculating coherency attributes.
Finally, the steering filter
regularization methodology needs to be tried in
conjunction with a variety of operators and
applied to real data problems.





Next: REFERENCES
Up: Clapp, et al.: Steering
Previous: REGULARIZATION
Stanford Exploration Project
9/12/2000