BASIC THEORY

Signal spectrum plus the noise spectrum gives the data spectrum. Since a prediction-error filter tends to the inverse of a spectrum we have

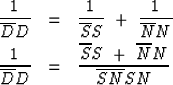
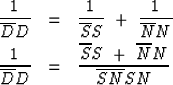$$\begin{eqnarray} {1\over \overline{D}D} &=& {1\over \overline{S}S} \ + \ {1... ... \overline{S}S} \ + \ { \overline{N}N} \over { \overline{SN} SN}\end{eqnarray}$$ (1) (2)

or  

$$\overline{D}D \quad =\quad { { \overline{SN} SN} \over { \overline{S}S} \ + \ { \overline{N}N} }$$ (3)

Now we are ready for the Spitz approximation. Spitz builds his applications upon the assumption that we can estimate D and N from suitable chunks of raw data. His result may be obtained from (3) by ignoring its denominator getting $D\approx SN$ or

$$S \quad\approx\quad D/N$$ (4)

Ignoring the denominator in equation (3), is not so terrible an approximation as it might seem. Remember that PEFs are important where they are small because they are used as weighting functions. Where weighting functions are small, solutions are expected to be large. Although Claerbout's assumption $S\approx D$ might be somewhat valid for signal and data spectra, it is much less valid for their PEFs. In practice, signal unpolluted with noise is usually not available. Even a very good chunk of data tends to yield a poor estimate of the signal PEF S because the holes in the signal spectrum are easily intruded with noise.

Obviously the major difference between $S\approx D$ and $S\approx D/N$ is where the noise is large. Thus it is for ``organized and predictable'' noises (small N) where we expect to see the main difference.

Theoretically, we need not make the Spitz approximation. We could solve (1) for S by spectral factorization. Although the S obtained would be more theoretically satisfying, there would be some practical disadvantages. Getting the signal spectrum by subtracting that of the noise from that of the data leaves the danger of a negative result (which explodes the factorization). Thus, maintaining spectral positivity would require extra care. All these extra burdens are avoided by making the Spitz approximation. All the more so in applications with continuously varying estimates.