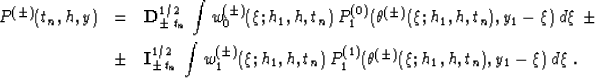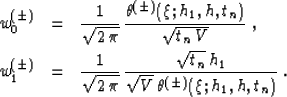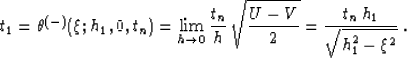Next: OFFSET CONTINUATION AND DMO
Up: Fomel: Offset continuation
Previous: THE CAUCHY PROBLEM
The integral solution of problem (1)-(3) is
obtained in Appendix A with the help of the classic methods of
mathematical physics. It takes the explicit form
| 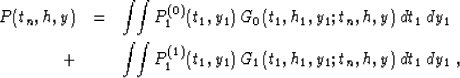 |
|
| (4) |
where the ``Green's functions'' G0 and G1 are expressed as
| 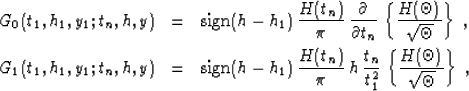 |
(5) |
| (6) |
and the parameter 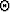 is
is
| 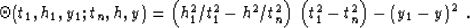 |
(7) |
H stands for the Heavyside step-function.
From formulas (5) and (6) one can see that the
impulse response of the offset continuation operator is discontinuous
in the time-offset-midpoint space on a surface defined by the equality
| 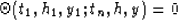 |
(8) |
that describes the ``wavefronts'' of the offset continuation process.
In terms of the theory of characteristics Courant (1962), the surface
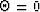 corresponds to the characteristic conoid formed by
bi-characteristics of equation (1) - ``time rays''
Fomel (1995) emerging from the point
corresponds to the characteristic conoid formed by
bi-characteristics of equation (1) - ``time rays''
Fomel (1995) emerging from the point 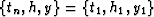 (Figure 1).
offcon
(Figure 1).
offcon
Figure 1
Constant-offset sections of the characteristic conoid - ``offset
continuation fronts'' (left), and branches of the conoid used in the
integral OC operator (right). The upper part of the plots
(small times) corresponds to continuation to smaller offsets; the
lower part (large times) corresponds to larger offsets.





As a second-order differential equation of the hyperbolic type, equation
(1) describes two different processes. The first
process is ``forward'' continuation from smaller to larger offsets;
the second one is ``reverse'' continuation in the opposite direction.
These two processes are clearly separated in the high-frequency
asymptotics of operator (4). To obtain the asymptotic
representation, it is sufficient to note that 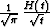 is the impulse response of the causal half-order
integration operator, and that
is the impulse response of the causal half-order
integration operator, and that 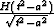 is
asymptotically equivalent to
is
asymptotically equivalent to 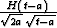 (t, a >0). Thus, the asymptotic form of the integral offset continuation
operator becomes
(t, a >0). Thus, the asymptotic form of the integral offset continuation
operator becomes
| 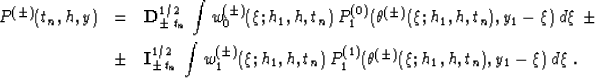 |
|
| (9) |
Here the signs ``+'' and ``-'' correspond to the type of
continuation (the sign of h-h1); 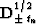 and
and
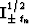 stand for the operators of causal and
anticausal half-order differentiation and integration applied with
respect to the time variable tn; the summation paths
stand for the operators of causal and
anticausal half-order differentiation and integration applied with
respect to the time variable tn; the summation paths
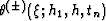 correspond to the two non-negative
sections of the characteristic conoid (8) (Figure
1):
correspond to the two non-negative
sections of the characteristic conoid (8) (Figure
1):
| 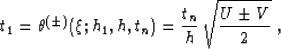 |
(10) |
where 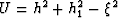 , and
, and 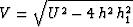 ;
; 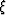 is
the midpoint separation (the integration parameter); and
is
the midpoint separation (the integration parameter); and 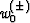 and
and 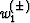 are the following weighting functions:
are the following weighting functions:
| 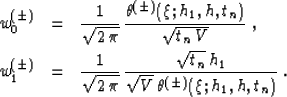 |
(11) |
| (12) |
Expression (10) for the summation path of the OC operator
was obtained previously by Stovas and Fomel 1993 and
Biondi and Chemingui . A somewhat
different form of it is proposed by Bagaini et
al. 1994. I describe the kinematic interpretation
of formula (10) in Appendix B.
The limit of expression (10) for the output offset h
approaching zero can be evaluated by L'Hospitale's rule. As one would
expect, it coincides with the well-known expression for the summation
path of the integral DMO operator
Deregowski and Rocca (1981)
| 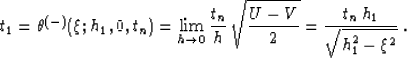 |
(13) |





Next: OFFSET CONTINUATION AND DMO
Up: Fomel: Offset continuation
Previous: THE CAUCHY PROBLEM
Stanford Exploration Project
4/19/2000
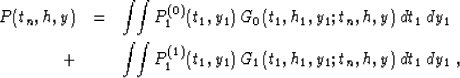
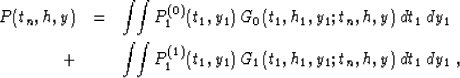
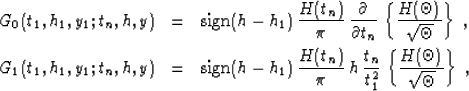
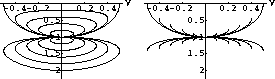
![]() is the impulse response of the causal half-order
integration operator, and that
is the impulse response of the causal half-order
integration operator, and that ![]() is
asymptotically equivalent to
is
asymptotically equivalent to ![]() (t, a >0). Thus, the asymptotic form of the integral offset continuation
operator becomes
(t, a >0). Thus, the asymptotic form of the integral offset continuation
operator becomes